五. Sorting and Searching

Posted on | In | Visitors: 
1
对应本书第五章。

原目录

笔记

这章开始进入算法部分，讲解排序和查找。

二分查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from __future__ import print_function

def binarySearch(alist, item):
    first = 0
    last = len(alist)-1
    found = False

    while first<=last and not found:
        midpoint = (first + last)//2
        if alist[midpoint] == item:
            found = True
        else:
            if item < alist[midpoint]:
                last = midpoint-1
            else:
                first = midpoint+1

    return found

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binarySearch(testlist, 3))
print(binarySearch(testlist, 13))
1
2
False
True

用Hash实现一个Map抽象数据类型

Hash碰到collision的时候一般有两种解决方法：

  • 开放寻址（open addressing）：寻找下一个空的slot；
  • 链接法（Chaining）：允许一个hash值对应的slot中可以存放多个元素。

使用Hash的Map，查找的理想的时间复杂度是$O(1)$。

实际上，对于占用度是$λ$的HashTable，开放寻址的线性探测的比较次数是：$\frac{1}{2}(1+\frac{1}{1−λ})$；链接法的比较次数是：$\frac{1}{2}(1+(\frac{1}{1−λ})^2)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class HashTable:
    
    def __init__(self):
        self.size = 11
        self.slots = [None] * self.size
        self.data = [None] * self.size
        
    def put(self,key,data):
        # 计算key的hash值
        hashvalue = self.hashfunction(key,len(self.slots))

        if self.slots[hashvalue] == None:
            self.slots[hashvalue] = key
            self.data[hashvalue] = data
        else:
            if self.slots[hashvalue] == key:
                self.data[hashvalue] = data  #replace
            else:
                # 碰到collision， rehash
                nextslot = self.rehash(hashvalue,len(self.slots))
                while self.slots[nextslot] != None and self.slots[nextslot] != key:
                    nextslot = self.rehash(nextslot,len(self.slots))

                if self.slots[nextslot] == None:
                    self.slots[nextslot]=key
                    self.data[nextslot]=data
                else:
                    self.data[nextslot] = data #replace

    def hashfunction(self,key,size):
        # 根据key计算hash值
        return key%size

    def rehash(self,oldhash,size):
        return (oldhash+1)%size

    def get(self,key):
        startslot = self.hashfunction(key,len(self.slots))

        data = None
        stop = False
        found = False
        position = startslot
        while self.slots[position] != None and not found and not stop:
            if self.slots[position] == key:
                found = True
                data = self.data[position]
            else:
                position=self.rehash(position,len(self.slots))
                if position == startslot:
                    stop = True
        return data

    def __getitem__(self,key):
        return self.get(key)

    def __setitem__(self,key,data):
        self.put(key,data)
1
2
3
4
5
6
7
8
9
10
11
H=HashTable()
H[54]="cat"
H[26]="dog"
H[93]="lion"
H[17]="tiger"
H[77]="bird"
H[31]="cow"
H[44]="goat"
H[55]="pig"
H[20]="chicken"
H.slots
1
[77, 44, 55, 20, 26, 93, 17, None, None, 31, 54]
1
H.data
1
2
3
4
5
6
7
8
9
10
11
['bird',
 'goat',
 'pig',
 'chicken',
 'dog',
 'lion',
 'tiger',
 None,
 None,
 'cow',
 'cat']

冒泡排序

默认从小到大排序。 两两比较，逆序则两两互换。

时间复杂度：$O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
def bubbleSort(alist):
    for passnum in range(len(alist)-1,0,-1):
        for i in range(passnum):
            # 逆序
            if alist[i]>alist[i+1]:
                # 互换
                temp = alist[i]
                alist[i] = alist[i+1]
                alist[i+1] = temp

alist = [54,26,93,17,77,31,44,55,20]
bubbleSort(alist)
print(alist)
1
[17, 20, 26, 31, 44, 54, 55, 77, 93]

选择排序

每次找到第k大的数，移动到倒数第k位。

时间复杂度：$O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def selectionSort(alist):
    for fillslot in range(len(alist)-1,0,-1):
        positionOfMax=0
        for location in range(1,fillslot+1):
            if alist[location]>alist[positionOfMax]:
                positionOfMax = location

        temp = alist[fillslot]
        alist[fillslot] = alist[positionOfMax]
        alist[positionOfMax] = temp

alist = [54,26,93,17,77,31,44,55,20]
selectionSort(alist)
print(alist)
1
[17, 20, 26, 31, 44, 54, 55, 77, 93]

插入排序

递归思想，前面的子序列先排完序，再插入下一个元素排序。

时间复杂度：$O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def insertionSort(alist):
    for index in range(1,len(alist)):

        currentvalue = alist[index]
        position = index

        while position>0 and alist[position-1]>currentvalue:
            # 大于插入元素的元素后移
            alist[position]=alist[position-1]
            # 插入元素前移
            position = position-1

        alist[position]=currentvalue

alist = [54,26,93,17,77,31,44,55,20]
insertionSort(alist)
print(alist)
1
[17, 20, 26, 31, 44, 54, 55, 77, 93]

希尔排序

使用由大到小的gap，将将list分割成几个sublist，对每个sublist做插入排序。

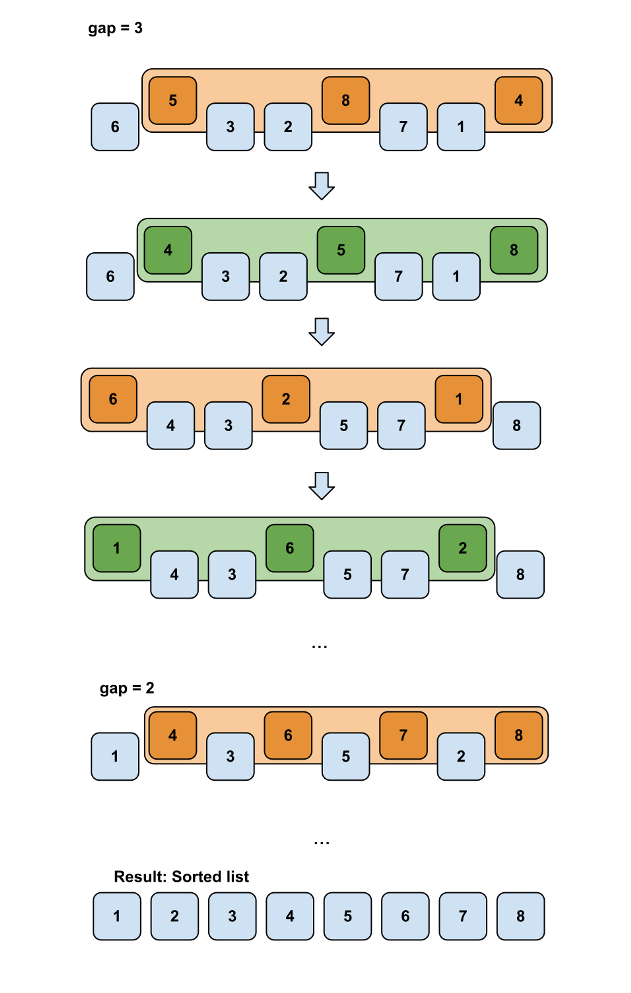
时间复杂度：介于$O(n)$和$O(n^2)$之间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def shellSort(alist):
    # gap为len的一半， gap等于sublistcount
    sublistcount = len(alist)//2
    while sublistcount > 0:

        for startposition in range(sublistcount):
            gapInsertionSort(alist,startposition,sublistcount)

        print("After increments of size",sublistcount,
                                   "The list is",alist)

        # gap再减半
        sublistcount = sublistcount // 2

def gapInsertionSort(alist,start,gap):
    # 对sublist进行插入排序
    for i in range(start+gap,len(alist),gap):

        currentvalue = alist[i]
        position = i

        while position>=gap and alist[position-gap]>currentvalue:
            alist[position]=alist[position-gap]
            position = position-gap

        alist[position]=currentvalue
        
alist = [54,26,93,17,77,31,44,55,20]
shellSort(alist)
print(alist)
1
2
3
4
After increments of size 4 The list is [20, 26, 44, 17, 54, 31, 93, 55, 77]
After increments of size 2 The list is [20, 17, 44, 26, 54, 31, 77, 55, 93]
After increments of size 1 The list is [17, 20, 26, 31, 44, 54, 55, 77, 93]
[17, 20, 26, 31, 44, 54, 55, 77, 93]

合并排序

递归地将一个list拆分成两个sublist，然后merge。

时间复杂度是：$O(nlogn)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def mergeSort(alist):
    print("Splitting ",alist)
    if len(alist)>1:
        # 拆分成两个子序列
        mid = len(alist)//2
        # 注意：使用切片的方式空间复杂度较高
        lefthalf = alist[:mid]
        righthalf = alist[mid:]

        mergeSort(lefthalf)
        mergeSort(righthalf)

        # 执行merge
        i=0
        j=0
        k=0
        while i < len(lefthalf) and j < len(righthalf):
            if lefthalf[i] < righthalf[j]:
                alist[k]=lefthalf[i]
                i=i+1
            else:
                alist[k]=righthalf[j]
                j=j+1
            k=k+1

        while i < len(lefthalf):
            alist[k]=lefthalf[i]
            i=i+1
            k=k+1

        while j < len(righthalf):
            alist[k]=righthalf[j]
            j=j+1
            k=k+1
    print("Merging ",alist)

alist = [54,26,93,17,77,31,44,55,20]
mergeSort(alist)
print(alist)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
Splitting  [54, 26, 93, 17, 77, 31, 44, 55, 20]
Splitting  [54, 26, 93, 17]
Splitting  [54, 26]
Splitting  [54]
Merging  [54]
Splitting  [26]
Merging  [26]
Merging  [26, 54]
Splitting  [93, 17]
Splitting  [93]
Merging  [93]
Splitting  [17]
Merging  [17]
Merging  [17, 93]
Merging  [17, 26, 54, 93]
Splitting  [77, 31, 44, 55, 20]
Splitting  [77, 31]
Splitting  [77]
Merging  [77]
Splitting  [31]
Merging  [31]
Merging  [31, 77]
Splitting  [44, 55, 20]
Splitting  [44]
Merging  [44]
Splitting  [55, 20]
Splitting  [55]
Merging  [55]
Splitting  [20]
Merging  [20]
Merging  [20, 55]
Merging  [20, 44, 55]
Merging  [20, 31, 44, 55, 77]
Merging  [17, 20, 26, 31, 44, 54, 55, 77, 93]
[17, 20, 26, 31, 44, 54, 55, 77, 93]

快速排序

递归地执行：小的元素移到pivot左边，大的元素移到pivot的右边。

类比军训时，教官会找出一个同学说，以这位同学为基准，矮的站右边，高的站右边。

一般在实现的时候，上面提到的这步使用双指针的技巧实现。
时间复杂度是：$O(nlogn)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
def quickSort(alist):
    quickSortHelper(alist,0,len(alist)-1)

def quickSortHelper(alist,first,last):
    if first<last:

        # 执行军训排序部分
        splitpoint = partition(alist,first,last)
        # 递归地对子序列进行排序
        quickSortHelper(alist,first,splitpoint-1)
        quickSortHelper(alist,splitpoint+1,last)


def partition(alist,first,last):
    # 第一个元素作为标杆
    pivotvalue = alist[first]

    # 使用双指针从两边向中间靠拢
    leftmark = first+1
    rightmark = last

    done = False
    while not done:

        while leftmark <= rightmark and alist[leftmark] <= pivotvalue:
            leftmark = leftmark + 1

        while alist[rightmark] >= pivotvalue and rightmark >= leftmark:
            rightmark = rightmark -1

        if rightmark < leftmark:
            done = True
        else:
            # 空间复杂度是1
            temp = alist[leftmark]
            alist[leftmark] = alist[rightmark]
            alist[rightmark] = temp

    temp = alist[first]
    alist[first] = alist[rightmark]
    alist[rightmark] = temp
    return rightmark

alist = [54,26,93,17,77,31,44,55,20]
quickSort(alist)
print(alist)

作业

作业原地址

q1

计算装填因子$λ$分别是：0.1, 0.25, 0.5, 0.75, 0.9, 0.99时需要的比较次数。

计算公式：$\frac{1}{2}(1+\frac{1}{1−λ})$。

直接封装一个函数：

1
2
3
4
5
6
def hash_compare(load_fraction):
    lam = (1 + 1./(1-load_fraction)) / 2
    return lam

for i in [0.1, 0.25, 0.5, 0.75, 0.9, 0.99]:
    print(i, " : ", hash_compare(i))
1
2
3
4
5
6
0.1  :  1.05555555556
0.25  :  1.16666666667
0.5  :  1.5
0.75  :  2.5
0.9  :  5.5
0.99  :  50.5

q2

设计计算字符串的hash值的hash函数。

使用positional weight：

1
2
3
4
5
6
7
8
9
10
11
12
def hash_function_4str(key_str, size):
    hash_value = 0
    for i, c in enumerate(key_str):
        hash_value += (i+1)* ord(c)
    print(hash_value)
    hash_value %= size
    print(hash_value)
    return hash_value
        
        
hash_function_4str("cat", 11)
hash_function_4str("happy", 11)
1
2
3
4
5
6
641
3
1687
4

4

q4

调研string的hash函数：

参考这篇博客

q9

修改快排中pivot的位置（原算法的pivot是第一个元素，题目推荐尝试中间元素），对比性能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
def quickSort(alist):
    quickSortHelper(alist,0,len(alist)-1)

def quickSortHelper(alist,first,last):
    if first<last:

        # 执行军训排序部分
        splitpoint = partition(alist,first,last)
        # 递归地对子序列进行排序
        quickSortHelper(alist,first,splitpoint-1)
        quickSortHelper(alist,splitpoint+1,last)


def partition(alist,first,last):
    # 中间的元素作为标杆
    pivotindex = (first + last) / 2
    pivotvalue = alist[pivotindex]

    # 使用双指针从两边向中间靠拢
    leftmark = first
    rightmark = last

    done = False
    print("pivotvalue: ", pivotvalue)
    while not done:
        while leftmark <= rightmark and alist[leftmark] <= pivotvalue:
            leftmark = leftmark + 1

        while alist[rightmark] >= pivotvalue and rightmark >= leftmark and rightmark > first:
            rightmark = rightmark -1

        if rightmark < leftmark or rightmark == first:
            done = True
        else:
            # 空间复杂度是1
            temp = alist[leftmark]
            alist[leftmark] = alist[rightmark]
            alist[rightmark] = temp
    temp = alist[pivotindex]
    alist[pivotindex] = alist[rightmark]
    alist[rightmark] = temp
    return leftmark

alist = [54,26,93,17,77,31,44,55,20]
quickSort(alist)
# partition(alist,0, 8)
print(alist)
1
2
3
4
5
6
7
8
pivotvalue:  77
pivotvalue:  17
pivotvalue:  55
pivotvalue:  54
pivotvalue:  31
pivotvalue:  20
pivotvalue:  26
[17, 20, 26, 31, 44, 54, 55, 77, 93]

pivot设置在中间位置可以让已经排好序的list不用再做交换操作。