六. Trees and Tree Algorithms

Posted on | In | Visitors: 
1
对应本书第六章。

原目录

笔记

作者介绍了两个计算机中的树结构：文件系统（File System）和HTML页面。

用结点和引用实现的二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from __future__ import print_function

class BinaryTree:
    def __init__(self,rootObj):
        self.key = rootObj
        self.leftChild = None
        self.rightChild = None

    def insertLeft(self,newNode):
        if self.leftChild == None:
            self.leftChild = BinaryTree(newNode)
        else:
            t = BinaryTree(newNode)
            t.leftChild = self.leftChild
            self.leftChild = t

    def insertRight(self,newNode):
        if self.rightChild == None:
            self.rightChild = BinaryTree(newNode)
        else:
            t = BinaryTree(newNode)
            t.rightChild = self.rightChild
            self.rightChild = t

    def getRightChild(self):
        return self.rightChild

    def getLeftChild(self):
        return self.leftChild

    def setRootVal(self,obj):
        self.key = obj

    def getRootVal(self):
        return self.key
1
2
3
4
5
6
7
8
9
10
11
r = BinaryTree('a')
print(r.getRootVal())
print(r.getLeftChild())
r.insertLeft('b')
print(r.getLeftChild())
print(r.getLeftChild().getRootVal())
r.insertRight('c')
print(r.getRightChild())
print(r.getRightChild().getRootVal())
r.getRightChild().setRootVal('hello')
print(r.getRightChild().getRootVal())
1
2
3
4
5
6
7
a
None
<__main__.BinaryTree instance at 0x7f55e658a320>
b
<__main__.BinaryTree instance at 0x7f55e33bedd0>
c
hello

解析树

Parse Tree的构建规则（这里是数学表达式的解析树）：

  • 如果当前token是'('，增加一个结点作为左子结点，下降到左子结点。
  • 如果当前token属于['+','-','/','*']，将当前结点的值设为这个操作符，增加一个结点作为右子结点，下降到右子结点。
  • 如果当前token是一个数字，则将当前结点的值设为这个数字，回到父结点。
  • 如果当前token是')'，回到父结点。

构建的解析树如下：

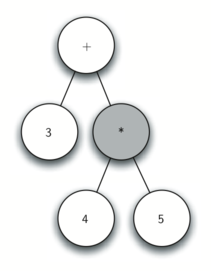
构建解析树的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from pythonds.basic.stack import Stack
from pythonds.trees.binaryTree import BinaryTree

def buildParseTree(fpexp):
    fplist = fpexp.split()
    pStack = Stack()
    eTree = BinaryTree('')
    pStack.push(eTree)
    currentTree = eTree
    for i in fplist:
        # 如果当前token是`'('`，增加一个结点作为左子结点，下降到左子结点。
        if i == '(':
            currentTree.insertLeft('')
            pStack.push(currentTree)
            currentTree = currentTree.getLeftChild()
        # 如果当前token是一个数字，则将当前结点的值设为这个数字，回到父结点。
        elif i not in ['+', '-', '*', '/', ')']:
            currentTree.setRootVal(int(i))
            parent = pStack.pop()
            currentTree = parent
        # 如果当前token属于`['+','-','/','*']`，将当前结点的值设为这个操作符，增加一个结点作为右子结点，下降到右子结点。
        elif i in ['+', '-', '*', '/']:
            currentTree.setRootVal(i)
            currentTree.insertRight('')
            pStack.push(currentTree)
            currentTree = currentTree.getRightChild()
        # 如果当前token是`')'`，回到父结点。
        elif i == ')':
            currentTree = pStack.pop()
        else:
            raise ValueError
    return eTree

pt = buildParseTree("( 3 + ( 4 * 5 ) )")
pt.postorder()  #defined and explained in the next section
1
2
3
4
5
3
4
5
*
+

计算表达式的值：

1
2
3
4
5
6
7
8
9
10
11
12
13
import operator
def evaluate(parseTree):
    opers = {'+':operator.add, '-':operator.sub, '*':operator.mul, '/':operator.truediv}

    leftC = parseTree.getLeftChild()
    rightC = parseTree.getRightChild()

    if leftC and rightC:
        fn = opers[parseTree.getRootVal()]
        return fn(evaluate(leftC),evaluate(rightC))
    else:
        return parseTree.getRootVal()
evaluate(pt)
1
23

树的遍历

1.前序遍历（preorder），即根左右。

1
2
3
4
5
def preorder(tree):
    if tree:
print(tree.getRootVal())
        preorder(tree.getLeftChild())
preorder(tree.getRightChild())

2.中序遍历（inorder），即左根右。

1
2
3
4
5
6
def
inorder(tree):
  if tree != None:
      inorder(tree.getLeftChild())
print(tree.getRootVal())
      inorder(tree.getRightChild())

3.后序遍历（postorder），即左右根。

1
2
3
4
5
def postorder(tree):
    if tree != None:
postorder(tree.getLeftChild())
        postorder(tree.getRightChild())
print(tree.getRootVal())

4.层次遍历，即：根/子子/孙孙孙孙

原书没有提及层次遍历，这里做一点补充。

1
2
3
4
5
6
7
8
9
10
11
def level_order(tree):
    # 维护一个队列
    trav_queue = []
    trav_queue.insert(0, tree)
    while len(trav_queue) != 0:
        cur_node = trav_queue.pop()
        if cur_node.getLeftChild():
            trav_queue.insert(0, cur_node.getLeftChild())
        if cur_node.getRightChild():
            trav_queue.insert(0, cur_node.getRightChild())
        print(cur_node.getRootVal())
1
2
3
4
5
6
7
8
9
10
11
12
# 对比前序遍历和层次遍历的区别
def preorder(tree):
    if tree:
        print(tree.getRootVal())
        preorder(tree.getLeftChild())
        preorder(tree.getRightChild())
r = BinaryTree('a')
r.insertLeft('b')
r.insertRight('c')
r.getLeftChild().insertLeft('d')
r.getLeftChild().insertLeft('e')
preorder(r)
1
2
3
4
5
a
b
e
d
c
1
level_order(r)
1
2
3
4
5
a
b
c
e
d

二叉堆

首先引入priority queue的概念，你可以把它想象成操作系统中优先级队列，它的特征是：每一次出队的是优先级最高的元素。

如果你使用list实现它，每一次出队前需要重新排序，那么时间复杂度可能是$O(nlogn)$。或者你可以说，只需要第一次排个序就可以，后面每入队一个元素的时候，都加到合适的位置里去，这样插入一个元素的时间复杂度是$O(n)$。

计算机科学家觉得还是不够，于是发明了二叉堆，使得优先级队列的时间复杂度是$O(logn)$。

二叉堆从外观上来看是一棵完全二叉树，但它有一个性质，即父结点比子结点小（小顶堆）。

接下来看看如何实现一个二叉堆：

需要实现的方法：

实现的时候，首先牢记二叉堆的两个属性：

  1. The StructureProperty，即二叉堆在结构上是一棵完全二叉树。原因是完全二叉树可以直接存在list中。第0个元素置空，第$i$个元素的左子结点和右子结点分别是$i×2$和$i×2+1$，第i个元素的父结点是$i/2$。
  2. Heap Order Property，即父结点比子结点小。

主要关注两个过程，注意过程中要维护上面的两个属性：

  1. 插入元素时的percolate up，即结点比父结点大的，和父结点互换。
  2. 删除元素时的percolatedown，即删除顶结点以后，先将最后一个结点补入第一位，然后再不断地将这个结点跟其最小的子结点比，大于这个子结点则互换。
  3. 这里如果忘了，最好回去看原文，有很生动的图，一看就懂。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class BinHeap:
    def __init__(self):
        self.heapList = [0]
        self.currentSize = 0
        
    def percUp(self,i):
        while i // 2 > 0:
            if self.heapList[i] < self.heapList[i // 2]:
                tmp = self.heapList[i // 2]
                self.heapList[i // 2] = self.heapList[i]
                self.heapList[i] = tmp
            i = i // 2
            
    def insert(self,k):
        self.heapList.append(k)
        self.currentSize = self.currentSize + 1
        self.percUp(self.currentSize)
        
    def percDown(self,i):
        while (i * 2) <= self.currentSize:
            mc = self.minChild(i)
            if self.heapList[i] > self.heapList[mc]:
                tmp = self.heapList[i]
                self.heapList[i] = self.heapList[mc]
                self.heapList[mc] = tmp
            i = mc

    def minChild(self,i):
        if i * 2 + 1 > self.currentSize:
            return i * 2
        else:
            if self.heapList[i*2] < self.heapList[i*2+1]:
                return i * 2
            else:
                return i * 2 + 1
            
    def delMin(self):
        retval = self.heapList[1]
        self.heapList[1] = self.heapList[self.currentSize]
        self.currentSize = self.currentSize - 1
        self.heapList.pop()
        self.percDown(1)
        return retval
    
    def buildHeap(self,alist):
        i = len(alist) // 2
        self.currentSize = len(alist)
        self.heapList = [0] + alist[:]
        while (i > 0):
            self.percDown(i)
            i = i - 1

二叉查找树

二叉查找树（bst）即这样的二叉树：

所有的父结点的值都比左子结点的大，但比右子结点的小。
值得注意的是bst的删除操作，分三种情况：

1.该目标结点没有子节点；

这种情况直接删除目标结点即可。

2.该目标结点只有一个子节点；

这种情况需要先将目标结点删除，再把目标结点的子结点连到目标结点的父结点上

3.该目标结点有两个子节点。

这种情况最复杂，删除目标结点后，需要寻找successor，来替代当前结点的位置。

successor必须满足比目标结点所有左子树要大，比所有右子树要小，又分三种情况：

  1. 目标结点有右子结点，则successor是右子树的最小结点（这个结点是比目标结点大的最小结点）。上面图示就是这种情况。
  2. 目标结点没有右子结点，且是父结点的左子结点，这说明父结点小于目标结点的所有左子树，则successor直接选用目标结点的父结点。
  3. 目标结点没有右子结点，且是父结点的右子结点，这说明父结点大于目标结点的所有左子树，则递归地再去寻找父结点的successor。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
class TreeNode:
    """helper类"""
    def __init__(self,key,val,left=None,right=None,parent=None):
        self.key = key
        self.payload = val
        self.leftChild = left
        self.rightChild = right
        self.parent = parent

    def hasLeftChild(self):
        return self.leftChild

    def hasRightChild(self):
        return self.rightChild

    def isLeftChild(self):
        return self.parent and self.parent.leftChild == self

    def isRightChild(self):
        return self.parent and self.parent.rightChild == self

    def isRoot(self):
        return not self.parent

    def isLeaf(self):
        return not (self.rightChild or self.leftChild)

    def hasAnyChildren(self):
        return self.rightChild or self.leftChild

    def hasBothChildren(self):
        return self.rightChild and self.leftChild

    def replaceNodeData(self,key,value,lc,rc):
        self.key = key
        self.payload = value
        self.leftChild = lc
        self.rightChild = rc
        if self.hasLeftChild():
            self.leftChild.parent = self
        if self.hasRightChild():
            self.rightChild.parent = self


class BinarySearchTree:

    def __init__(self):
        self.root = None
        self.size = 0

    def length(self):
        return self.size

    def __len__(self):
        return self.size

    def put(self, key, val):
        if self.root:
            self._put(key, val, self.root)
        else:
            self.root = TreeNode(key,val)
        self.size = self.size + 1

    def _put(self, key, val, currentNode):
        # 小于当前结点的值放入左子树，否则放入右子树
        if key < currentNode.key:
            if currentNode.hasLeftChild():
                 self._put(key, val, currentNode.leftChild)
            else:
                 currentNode.leftChild = TreeNode(key,val,parent=currentNode)
        else:
            if currentNode.hasRightChild():
                 self._put(key,val,currentNode.rightChild)
            else:
                 currentNode.rightChild = TreeNode(key,val,parent=currentNode)

    def __setitem__(self,k,v):
        self.put(k,v)

    def get(self,key):
        if self.root:
            res = self._get(key,self.root)
            if res:
                return res.payload
            else:
                return None
        else:
            return None

    def _get(self,key,currentNode):
        if not currentNode:
            return None
        elif currentNode.key == key:
            return currentNode
        elif key < currentNode.key:
            return self._get(key,currentNode.leftChild)
        else:
            return self._get(key,currentNode.rightChild)

    def __getitem__(self, key):
        return self.get(key)

    def __contains__(self, key):
        if self._get(key, self.root):
            return True
        else:
            return False

    def delete(self, key):
        if self.size > 1:
            nodeToRemove = self._get(key, self.root)
            if nodeToRemove:
                self.remove(nodeToRemove)
                self.size = self.size-1
            else:
                raise KeyError('Error, key not in tree')
        elif self.size == 1 and self.root.key == key:
            self.root = None
            self.size = self.size - 1
        else:
            raise KeyError('Error, key not in tree')

    def __delitem__(self, key):
        self.delete(key)

    def spliceOut(self):
        if self.isLeaf():
            if self.isLeftChild():
                self.parent.leftChild = None
            else:
                self.parent.rightChild = None
        elif self.hasAnyChildren():
            if self.hasLeftChild():
                if self.isLeftChild():
                    self.parent.leftChild = self.leftChild
                else:
                    self.parent.rightChild = self.leftChild
                self.leftChild.parent = self.parent
            else:
                if self.isLeftChild():
                    self.parent.leftChild = self.rightChild
                else:
                    self.parent.rightChild = self.rightChild
                self.rightChild.parent = self.parent

    def findSuccessor(self):
        """
        1.结点有右子结点，则successor是右子树的最小结点。
        2.结点没有右子结点，且是父结点的左子结点，则successor是父结点。
        3.结点没有右子结点，且是父结点的右子结点，则successor是父结点的successor。
        """
        succ = None
        if self.hasRightChild():
            succ = self.rightChild.findMin()
        else:
            if self.parent:
                if self.isLeftChild():
                    succ = self.parent
                else:
                    self.parent.rightChild = None
                    succ = self.parent.findSuccessor()
                    self.parent.rightChild = self
        return succ

    def findMin(self):
        current = self
        while current.hasLeftChild():
            current = current.leftChild
        return current

    def remove(self,currentNode):
        """删除结点"""
        # 该结点没有子结点，即叶子节点，直接删去即可
        if currentNode.isLeaf(): #leaf      
            if currentNode == currentNode.parent.leftChild:
                currentNode.parent.leftChild = None
            else:
                currentNode.parent.rightChild = None
            
        # 该结点有两个子结点，最复杂
        elif currentNode.hasBothChildren(): #interior
            succ = currentNode.findSuccessor()
            succ.spliceOut()
            currentNode.key = succ.key
            currentNode.payload = succ.payload

        else: # 该结点只有一个子结点
            if currentNode.hasLeftChild():
                if currentNode.isLeftChild():
                    currentNode.leftChild.parent = currentNode.parent
                    currentNode.parent.leftChild = currentNode.leftChild
                elif currentNode.isRightChild():
                    currentNode.leftChild.parent = currentNode.parent
                    currentNode.parent.rightChild = currentNode.leftChild
                else:
                    # 该结点是root
                    currentNode.replaceNodeData(currentNode.leftChild.key,
                                    currentNode.leftChild.payload,
                                    currentNode.leftChild.leftChild,
                                    currentNode.leftChild.rightChild)
            else:
                if currentNode.isLeftChild():
                    currentNode.rightChild.parent = currentNode.parent
                    currentNode.parent.leftChild = currentNode.rightChild
                elif currentNode.isRightChild():
                    currentNode.rightChild.parent = currentNode.parent
                    currentNode.parent.rightChild = currentNode.rightChild
                else:
                    currentNode.replaceNodeData(currentNode.rightChild.key,
                                    currentNode.rightChild.payload,
                                    currentNode.rightChild.leftChild,
                                    currentNode.rightChild.rightChild)


mytree = BinarySearchTree()
mytree[3]="red"
mytree[4]="blue"
mytree[6]="yellow"
mytree[2]="at"

print(mytree[6])
print(mytree[2])
1
2
yellow
at

平衡二叉查找树

当一般的二叉查找树出现倾斜的情况（skewed tree）：

时间复杂度右重新变成了$O(n)$，于是引入平衡二叉查找树（Balanced Binary Search Trees， AVL tree），解决倾斜问题（AVL的命名源自其作者的名字）。

平衡因子（balance factor）：$balanceFactor=height(leftSubTree)−height(rightSubTree)$，即左子树的高度-右子树的高度。

如果一棵二叉查找树可以被称为平衡，则其所有子树的平衡因子只能是：-1,0,1三者之一。

先来看看AVL的性能：

来找到最左倾的AVL的结点个数和高度：

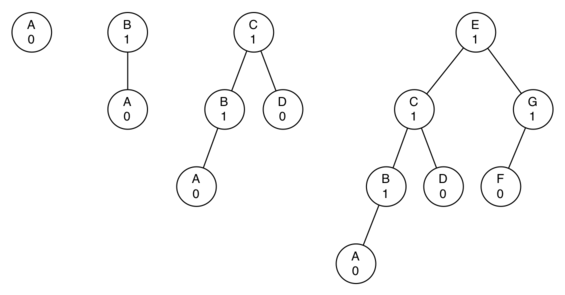
很容易可以发现一个规律，即$N_h=1+N_{h−1}+N_{h−2}$。其中，$h$是树的高度，$N_h$是高度$h$的情况下，最左倾的AVL的结点个数。这个形态和斐波那契数列是一致的。斐波那契数列有一个性质就是，对于足够大的数，后一个比前一个的比值接近于黄金分割：$Φ=\frac{1+\sqrt5}{2}$。

可以将递推公式转换成：$h=1.44logN_h$，也就是说，AVL的查找操作的复杂度，依然是：$O(logN)$。

现在考虑如何维护平衡，对插入元素的父结点递归地更新平衡因子，直到：1.已经更新到root；2.当前父结点的平衡因子是0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def
updateBalance(self,node):
    """更新平衡因子"""
    if node.balanceFactor > 1 or
node.balanceFactor < -1:
        self.rebalance(node)
        return
    if
node.parent != None:
        if node.isLeftChild():
node.parent.balanceFactor += 1
        elif node.isRightChild():
node.parent.balanceFactor -= 1

        if node.parent.balanceFactor != 0:
self.updateBalance(node.parent)

获得新的平衡因子以后，需要对不平衡的结点做旋转（操作）。

左旋：

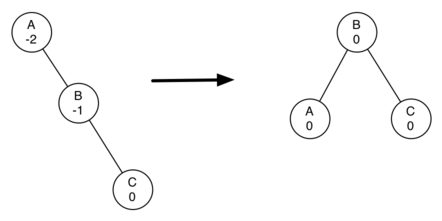
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def rotateLeft(self,rotRoot):
    # 当前根结点的右子结点变成新的根节点
    newRoot =
rotRoot.rightChild
    # 如果新根有左子树，移到当前根结点的右子树上
    rotRoot.rightChild =
newRoot.leftChild
    if newRoot.leftChild != None:
newRoot.leftChild.parent = rotRoot
    # 当前根的父结点传给新根
    newRoot.parent =
rotRoot.parent
    if rotRoot.isRoot():
        self.root = newRoot
    else:
if rotRoot.isLeftChild():
                rotRoot.parent.leftChild = newRoot
else:
            rotRoot.parent.rightChild = newRoot
    # 当前根变成新根的左子树
newRoot.leftChild = rotRoot
    rotRoot.parent = newRoot
    # 更新平衡参数
rotRoot.balanceFactor = rotRoot.balanceFactor + 1 - min(newRoot.balanceFactor,
0)
    newRoot.balanceFactor = newRoot.balanceFactor + 1 +
max(rotRoot.balanceFactor, 0)

最后两行的更新平衡参数需要补充解释：

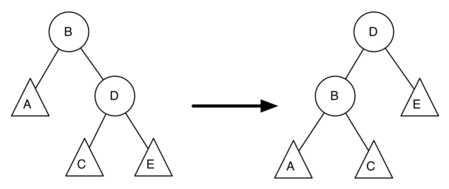
$newBal(B)=h_A−h_C$，

$oldBal(B)=h_A−h_D$，

对于旋转前：$h_D=1+max(h_C,h_E)$，而经过旋转后$h_C$和$h_E$是不变的。

于是有：$oldBal(B)=h_A−(1+max(h_C,h_E))$

再将两条表达式相减，有：

$$
newBal(B) - oldBal(B) = h_A - h_C - (h_A - (1 + max(h_C,h_E))) \
newBal(B) -
oldBal(B) = h_A - h_C - h_A + (1 + max(h_C,h_E)) \
newBal(B) - oldBal(B) = h_A

  • h_A + 1 + max(h_C,h_E) - h_C \
    newBal(B) - oldBal(B) = 1 + max(h_C,h_E) -
    h_C \
    newBal(B) = oldBal(B) + 1 + max(h_C - h_C ,h_E - h_C) \
    newBal(B) =
    oldBal(B) + 1 + max(0 , -oldBal(D)) \
    newBal(B) = oldBal(B) + 1 - min(0 ,
    oldBal(D)) \
    $$

即

1
2
rotRoot.balanceFactor = rotRoot.balanceFactor + 1 -
min(newRoot.balanceFactor, 0)

类似的方法可以推出：

1
2
newRoot.balanceFactor =
newRoot.balanceFactor + 1 + max(rotRoot.balanceFactor, 0)

还有一个问题，如果是这样的右倾：


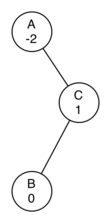
直接进行左旋，结果是：

结果变成了左倾。

因此在做旋转之前，比如左旋，先检查左子树是否左倾，如果有要先右旋左子树：

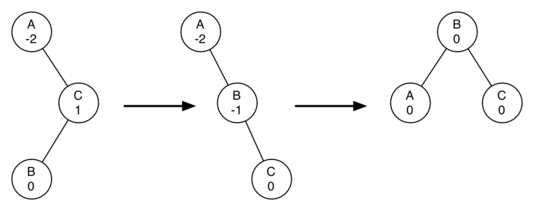
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def rebalance(self,node):
  if node.balanceFactor < 0:
         if
node.rightChild.balanceFactor > 0:
            self.rotateRight(node.rightChild)
self.rotateLeft(node)
         else:
            self.rotateLeft(node)
  elif
node.balanceFactor > 0:
         if node.leftChild.balanceFactor < 0:
self.rotateLeft(node.leftChild)
            self.rotateRight(node)
else:
            self.rotateRight(node)

讨论作业