Leetcode算法题攻略之Python

Posted on Edited on In

数组 Array

分类 leetcode 提示
哈希表 1. 两数之和
双指针 15. 三数之和 先排序
16. 最接近的三数之和 先排序
18. 四数之和
27. 移除元素 类似partition的交换
26. 删除排序数组中的重复项 不用交换，直接将需要的拷贝
283. 移动零 类似partition的交换
搜索 74. 搜索二维矩阵 从右上角开始开始缩小领域
240. 搜索二维矩阵 II 从左下角开始缩小领域
动态规划 53. 最大子序和
152. 乘积最大子序列
其他 238. 除自身以外数组的乘积 乘积 = 当前数左边的乘积 * 当前数右边的乘积

字符串 String

常用操作：

  • ord(c)：返回字符c对应的对于8位的ASCII数值。
  • chr(d)：返回ASCII数值对应的字符。

区分概念：

子字符串：连续；子序列：可以不连续。

典型题

字符串匹配 String Matching

字符串匹配算法：

  • KMP：
    • 永不回退文本串的指针i
    • 有限状态机
    • 二维状态跳转矩阵fsm[i][j]表示匹配串已匹配前i个字符的状态下，看到字符j应该回退至何处。
  • Sunday
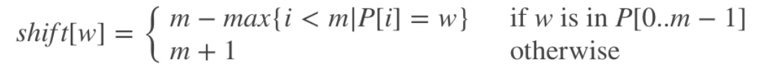
    • 偏移表：

典型题

回文 Palindrome

回文：从左往右读和从右往左读相同的字符串。

常用技巧：

  • 回文子串：遍历元素，每个元素都作为回文的中心出发（中心长度分1或2两种情况）。

典型题

字母异位词 Anagrams

一个词的字母异位词即拥有的字符和该词相同，但顺序不一定相同。

常用技巧

常用哈希表存储，{字符: 次数}，哈希表相同则互为字母异位词。

典型题

位运算 Bit

技巧

  • Python中的按位运算符：
    • 左移运算符 <<
    • 右移运算符>>
    • 按位与 &
    • 按位或 |
    • 按位翻转 ～
    • 按位异或 ^
  • 数字加上前缀0b表示是二进制数字：0b1111
  • 用format字符串获取一个int的binary表示：
    • f"{a:b}"：将a转换成binary的str。
    • f"{a:030b}"：将a转换成binary的str，并在前面补0使其总位数是30。
  • -i是i的取反+1。
  • 判断i的第u位是不是1：i >> u & 1

典型题

运算 leetcode
或运算 1318. 或运算的最小翻转次数
异或运算 461. 汉明距离

二分查找 Binary Search

排序 Sort

对不考察排序算法本身的题可以灵活使用sorted(key=...)。

栈 Stack

先进后出的数据结构。

python中用list实现即可。入栈是append()，出栈是pop()。

队列 Queue

先进先出的数据结构。

python中队列建议使用deque。

1
2
3
4
5
6
7
8
from collections import deque

# deque([iterable[, maxlen]])
queue = deque()
queue.appendleft(1)  # 入队
queue.appendleft(2)
print(queue.pop())  # 出队，输出1
print(queue.pop())  # 出队，输出2

链表 List Node

常用技巧：

  • 在第一个节点前增加一个空数据的头结点，使得对第一个节点和对其他所有的节点的操作保持一致。
  • 使用快慢指针、前后指针帮助和长度相关的操作。

典型题

链表操作 leetcode 提示
链表节点删除 237. 删除链表中的节点 正常思路：prev.next = cur.next；若看不到上一个节点prev，则可将值拷贝到当前节点，然后删除下一个节点cur.val=cur.next.val; cur.next = cur.next.next
单链表反转 206. 反转链表 递归或正序遍历(增设头结点)
92. 反转链表 II
寻找两个单链表相交的起始节点 160. 相交链表 先后指针
链表中环的检测 141. 环形链表 快慢指针
有序的链表合并 21. 合并两个有序链表 递归或正序遍历(增加头结点)
23. 合并K个排序链表 使用小顶堆
删除链表倒数第n个结点 19. 删除链表的倒数第N个节点 先后指针
求链表的中间结点 876. 链表的中间结点 快慢指针
链表排序 148. 排序链表 归并排序
23. 合并K个排序链表

树 Tree

树的遍历

遍历类型 leetcode 提示
中序遍历 94. 二叉树的中序遍历 递归和非递归
230. 二叉搜索树中第K小的元素
前序遍历 589. N叉树的前序遍历 递归和非递归
后序遍历 590. N叉树的后序遍历 递归和非递归
层次遍历 102. 二叉树的层次遍历 借助一个queue
103. 二叉树的锯齿形层次遍历

非递归方案：颜色标记法，用一个栈保存要搜索的节点。推荐阅读。

  • 白色：顶点没有被访问过。
  • 灰色：当顶点第一次被访问时，它就会被标记为灰色;
  • 黑色：当完成对该顶点的访问之后，它就会被标记为黑色。

树的深度

树的校验

树的特征：

  • 有向图的判断：除了根节点，每个非空节点的入度都为1。
  • 无向图的判断：任意两个节点都有且只有一条相连的路径。即：任何无环的连通图，就是一棵树。保证连通的同时确定无环，则必然是树。

典型题

其他树相关

操作 leetcode 提示
树的序列化 297. 二叉树的序列化与反序列化

二叉搜索树 BST, Binary Search Tree

重要特性：1.左子树所有元素都小于根节点，右子树所有元素都大于根节点。2.中序遍历是升序的。

堆 Heap

python自带heapq支持小顶堆。最小的元素总是在根结点：heap[0]。heapq操作的是一个list：将一个初始list进行heap化（原地操作）。

1
2
3
4
5
6
7
8
9
import heapq

l = [3,2,4,5,1]
heapq.heapify(l)
print(l)  # 输出： [1, 2, 4, 5, 3]
heapq.heappush(l, 0)
print(l)  # 输出： [0, 2, 1, 5, 3, 4]
print(heapq.heappop(l))  # 输出： 0
print(l)  # 输出： [1, 2, 4, 5, 3]

典型题

哈希表 HashTable

有序字典 Ordered Dict

有序字典综合了哈希表和链表，在Python中为OrderedDict，在Java中为LinkedHashMap。

OrderedDict特有的操作：

  • popitem(last=True)：如果last值为真，则按后进先出的顺序返回键值对，否则就按先进先出的顺序返回键值对。可用于lru的删除。
  • move_to_end(key,last=True)：将现有key移动到有序字典的首端或者末端。可用于lru当元素被再次访问时的提前。

典型题

前缀树 Trie 字典树

技巧

常用dict实现。

常规实现：

1
2
3
4
5
6
7
8
9
trie = dict()
leaves = []
for word in words:
    cur_dict = trie
    for c in word:
        if c not in cur_dict:
            cur_dict[c] = {}
        cur_dict = cur_dict[c]
    leaves.append(cur_dict)

极简实现：

1
2
Trie = lambda: collections.defaultdict(Trie)
leaves = [reduce(dict.__getitem__, word, trie) for word in words]

典型题

线段树 Segment Tree

线段树是一棵完美二叉树（perfect binary tree），擅长处理区间，一般对区间操作的时间复杂度是$O(logn)$。

线段树的每个节点维护对应区间的最小值。

支持的操作：

  • 1.给定范围，求其中所有元素的最小值。
  • 2.赋值更新一个元素。

实现：由于是完美二叉树，自然可以用array或者list来存储。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class SegmentTree:
    def __init__(self, values):
        self.data = [0 for _ in values] + values
        self.n = len(values)
        for idx in reversed(range(1, self.n)):
            self.data[idx] = min(self.data[2*idx], self.data[2*idx+1])

    def update(self, idx, value):
        idx += self.n
        self.data[idx] = value

        while idx > 1:
            idx //= 2
            self.data[idx] = min(self.data[2*idx], self.data[2*idx+1])

    def minimum(self, left, right):
        left += self.n
        right += self.n
        minimum = self.data[left]

        while left < right:
            if left % 2:
                minimum = min(minimum, self.data[left])
                left += 1
            if right % 2:
                right -= 1
                minimum = min(minimum, self.data[right])
            left //= 2
            right //= 2

        return minimum

推荐阅读：Efficient Segment Tree Tutorial

732. 我的日程安排表 III

树状数组 Binary Indexed Tree

BIT的每个节点维护对应区间元素之和。

支持操作：

  • 1.计算从起点到某个点之间所有元素之和。
  • 2.自加更新一个元素。

实现：

  • 可基于线段树实现，想象删除所有右子节点。
  • i & -i是获取i的二进制中最后一个1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class BIT:
    """Implementation of a Binary Indexed Tree (Fennwick Tree)"""

    def __init__(self, nums):
        """"Initialize BIT with nums in O(n)"""
        self.array = [0] + nums
        for idx in range(1, len(self.array)):
            idx2 = idx + (idx & -idx)
            if idx2 < len(self.array):
                self.array[idx2] += self.array[idx]

    def prefix_query(self, idx):
        """Computes prefix sum of up to including the idx-th element"""
        idx += 1
        result = 0
        while idx:
            result += self.array[idx]
            idx -= idx & -idx
        return result

    def range_query(self, from_idx, to_idx):
        """Computes the range sum between two indices (both inclusive)"""
        return self.prefix_query(to_idx) - self.prefix_query(from_idx - 1)

    def update(self, idx, add):
        """Add a value to the idx-th element"""
        idx += 1
        while idx < len(self.array):
            self.array[idx] += add
            idx += idx & -idx

推荐阅读：Tutorial: Binary Indexed Tree (Fenwick Tree)

并查集 Union Find

并查集常用于连通相关的问题。并查集是一种树型（V字形，子节点指向父节点）的数据结构，支持下面两种操作：

  • Find：确定元素属于哪一个子集。返回的是该集合的代表元素（根）。
  • Union：将两个子集合并成同一个集合。

对于一个大小为$n$的集合，任何$m$次union或find操作所需要的时间复杂度都 是$O((m+n) α(n))$，其中$α$是Ackermann 函数的反函数，一般可以视为常量4。

需要自实现，因此需要记住并查集的实现方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class UnionFind:
    def __init__(self, n):
        self.up = list(range(n))
        self.rank = [0 for _ in range(n)]
        
    def find(self, x):
        if self.up[x] == x:
            return x
        else:
            self.up[x] = self.find(self.up[x])
        return self.up[x]
        
    def union(self, x, y):
        repr_x = self.find(x)
        repr_y = self.find(y)
        if repr_x == repr_y:  # 已在同一个集合中
            return False
        if self.rank[repr_x] == self.rank[repr_y]:  # 若同两个集合rank相同，把y所属的集合挂在x所属的集合下，并将x所属的集合的rank增加1
            self.rank[repr_x] += 1
            self.up[repr_y] = repr_x
        elif self.rank[repr_x] > self.rank[repr_y]:  # 否则谁的rank大，谁是被挂的，rank不需要改变
            self.up[repr_y] = repr_x
        else:
            self.up[repr_x] = repr_y
        return True

常用技巧：

  • 使用find(a)和find(b)的比较来判断是否在一个子集内。
  • 统计find(a) == a的个数（根的个数）来判断有多少个子集

基础题

提高题

图 Graph

邻接表：顶点->相邻顶点列表

图的搜索

宽度优先搜索 广度优先搜索 Breadth First Search, BFS

思路类似于树的层次遍历，但由于图可能存在环，所以需要一个数据结构记录某个顶点是否访问过。

典型题目：

深度优先搜索 Depth First Search, DFS

使用递归和非递归。非递归借助一个栈实现。思路类似于树的前中后序遍历，但由于图可能存在环，所以需要一个数据结构记录某个顶点是否访问过。

BFS or DFS

用两种图搜索都能解决的问题：

Hierholzer算法

欧拉迹是指一条包含图中所有边的一条路径，该路径中所有的边会且仅会出现一次。Hierholzer算法用于在连通图寻找欧拉迹。

推荐阅读：Hierholzer算法

拓扑排序

拓扑排序根据有向无环图（DAG）生成一个包含所有顶点的线性序列，使得如果图 G 中有一条边为 (v, w) ，那么顶点 v 排在顶点 w 之前。

算法过程：

使用卡恩算法：维基百科，实现类似层次遍历。

典型题目：

最短路径

Floyd算法

经典多源最短路径算法。

Dijkstra算法

经典单源最短路径算法。实现通常借助一个小顶堆heapq，保存未检查的节点与其到起点的距离。

最小生成树

普里姆（Prim）算法

贪心增加顶点。

大致实现流程：从第一个顶点开始，找最近的未加入顶点（借助heapq）。遍历类似BFS（借助deque）。直到所有顶点都加入。

克鲁斯卡尔（Kruskal）算法

贪心增加边，保证无环。

大致实现流程：将所有边按长度升序排列；借助并查集（union find）判断两个顶点是否连接通了不同的子集，是则加入该边。直到加入边的个数等于顶点数-1。

典型题

强联通分量

强联通分量（Strongly Connected Component）：有向图顶点子集S，内部任意两个顶点都能找到一条相连的路径。且S加入其它任意顶点后，都不满足这个条件。称S是原图的一个强连通分量。

Kosaraju算法

核心思想：一个图的反向图和原图具有一样的强连通分量。

算法：

  • 对有向图G取逆，得到G的反向图Gr。
  • 利用深度优先搜索求出G的后续遍历顺序。
  • 对Gr按照上述后续遍历顺序进行深度优先搜索。
  • 同一个深度优先搜索递归子程序中访问的所有顶点都在同一个强连通分量内

Tarjan算法

DFN(u)是节点u在DFS的序号；Low(u)是从u出发能到达的最小DFN(v)。Low(u)相同的点围成强连通分量。若DFN(u)=Low(u)则从u开始的搜索树上的节点即一个强连通分量。

  • u通过边到达v：Low(u) = min(Low(u), Low(v))
  • u通过返祖边到达v（v还在栈中）：Low(u) = min(Low(u), DFN(v))

推荐阅读：

拓展：找到无向联通图中的桥（割点，双联通分量）

1
2
3
4
5
6
7
8
9
def tarjan(time_stamp, u, p):
    dfn = low[u] = time_stamp
    for v in adj[u]:
        if v != p:
            if not low[v]:  # v not visited
                time_stamp += 1
                tarjan(time_stamp, v, u)
                if low[v] > dfn: ans.append([u, v])
            low[u] = min(low[u], low[v])

典型题

滑动窗口 Sliding Window

滑动窗口的针对对象往往是一个字符串或者数组。一般题干会问是否有满足条件的子串或者子数组（连续的）。

滑动窗口又名尺取法，即反复推进区间的开头（缩）和结尾（伸）。

操作：常用双指针实现，维护一个头指针，一个尾指针。当满足条件时移动尾指针（伸）；不满足要求时移动头指针（缩），直到重新满足要求。

分析：一般找一个满足某条件的子串的暴力解法的时间复杂度是$O(n^2)$。但若这个子串的条件满足一定的剪枝条件：如s[i:j]满足无重复字符且s[i:j+1]不满足，可以预见到对于所有k>0，s[i:j+k]都不满足。所以这个时候，继续伸已经没有意义，直接考虑缩。若伸缩交换能找到满足条件的子串，可以使用滑动窗口的方法。此时时间复杂度是$O(n)$。

推荐阅读：

大致模板：

1
2
3
4
5
6
7
8
9
while end < len(s):
    ...
    while not condition_func():
        ...
        start += 1
        ...
    # while condition_func():
    #   end += 1
    end += 1

可能会用到Counter：用于字符串的字符计数。

1
2
3
4
5
6
from collections import Counter

c1 = Counter("abbc")  # {"a": 1, "b": 2, "c": 1}
c2 = Counter("ab")
c3 = c1 & c2  # {"a": 1, "b": 1}
c4 = c1 | c2  # {'a': 1, 'b': 2, 'c': 1}

基础题

提升题

回溯 Backtracking

基本思想：从一条路往前走，能进则进，不能进则退回来，换一条路再试。

建议：把搜索树大致画下，思路更清晰。回溯一般借助DFS来实现。

基础题

提升题

贪心算法 Greedy Algorithm

贪心算法对问题求解时，总是做出在当前看来是最好的选择。选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。

动态规划 Dynamic Programing

动态规划把原问题分解为相对简单的子问题，并将子问题答案记忆化存储，以便下次需要同一个子问题解之时直接查表。动态规划通常自底向上地求解所有子问题结果，最终获得原问题结果。常适用于有重叠子问题和最优子结构性质的问题。

难点在于状态函数和递推关系的确定。

基础题

递推公式简单直接。

leetcode 递推关系
70. 爬楼梯 F(i) = F(i-1) + F(i-2)
53. 最大子序和 F(i) = max{F(i-1) + v(i), v(i)}
62. 不同路径 F(i, j) = F(i-1, j) + F(i, j-1)
63. 不同路径 II F(i, j) = F(i-1, j) + F(i, j-1)
64. 最小路径和 F(i, j) = min{F(i-1, j), F(i, j-1)} + d(i, j)}
198. 打家劫舍 F(i) = max{F(i-3) + F(i-2)} + v(i)}

提升题

递推关系不明显。

leetcode 状态函数 递推关系
96. 不同的二叉搜索树 $F(i)$代表前i个结点构成不同的二叉搜索树个数 $F(i)= \sum_{j=1}^i F(j−1)⋅F(i-j)$
139. 单词拆分 $F(i)$代表字符串中前i个字符是否能由字典中单词构成
72. 编辑距离 $F(i, j)$代表word1[:i+1]位置转换成word2[:j+1]位置需要最少步数 F(i,j) = min{F(i-1,j-1), F(i-1,j), F(i,j-1)} + 1
516. 最长回文子序列 $F(i,j)$表示s第i个字符到第j个字符的子串最长回文长度 若s[i]==s[j]，F(i,j)=F(i+1,j-1)+2；否则F(i,j)=max{F(i+1,j),F(i,j-1)}
1143. 最长公共子序列 $F(i, j)$代表text1[:i+1]和text2[:j+1]之间的最长公共子序列 若text1[i]==text2[j]则F(i,j)=1+F(i-1,j-1);否则F(i,j)=max{F(i-1,j),F(i,j-1)}

多个状态函数

有的时候状态函数可能不只一个，最终结果可能是多个状态函数综合计算的结果。

leetcode 状态函数 递推关系 提示
42. 接雨水 max_left[i]代表从最左到i的最大长度；max_right[i]代表从右到i的最大长度 max_left[i] = max{max_left[i-1], height[i]}，max_right[i] = max{max_right[i+1], height[i]} ，Σi{min(max_left[i],max_right[i])−height[i]} max_right代表从右往左投影的面积；max_left代表从左往右投影的面积。二者相交部分，减去固有柱子面积，即水的面积。
256. 粉刷房子 $R[k]$表示第k个房子是红色的时候，前k个房子的最小花销；$B[k]$和$G[k]$定义类似 R[k] = min{B[k-1], G[k-1]} + cost[k][0]，B[k] = min{R[k-1], G[k-1]} + cost[k][1]，G[k] = min{R[k-1], B[k-1]} + cost[k][2]，result = min{R[n-1], B[n-1], G[n-1]} 此题像极解码器中的维特比算法

状态压缩

状态压缩即把一个二元状态组用二进制数来表示。如开灯或关灯，选取或没选取，奇数或偶数，这些都属于二元状态。而如果有N盏灯、N个选项或者N个数，这就变成了一个二元状态组。

之所以叫状态压缩是因为这个二元状态组可以用一个整数表示，方便了计算和维护。

leetcode 二元状态
1349. 参加考试的最大学生数 是否坐人
5337. 每个元音包含偶数次的最长子字符串 包含奇数或偶数个的第i个元音
1125. 最小的必要团队 是否包含第i个技能
691. 贴纸拼词 是否包含target的第i个字符

直接记忆子问题结果

动态规划总的来说是自底向上的，有的问题自顶向下分析更简单，则可以采用记忆子问题结果的方案。

技巧：

python中可以使用lru_cache装饰器来缓存子问题：

1
2
3
4
5
from functools import lru_cache

@lru_cache(None)
def func(i, j):
    ...

背包问题

推荐阅读：背包问题九讲

类型 状态定义 递推关系 相关leetcode 提示
0-1背包问题 $F(i, v)$代表只考虑前i种物品放进容量为v的背包的最大价值。 F(i, v) = max{F(i-1, v), F(i-1, v-C(i)) + W(i)} 416. 分割等和子集 问题转换成(sum/2)的容量的0-1背包。状态$F(i,v)$表示使用前i种物品能否完全填满背包。F(i,v)=F(i-1,v) or F(i-1,v-C(i))
完全背包 同上 F(i, v) = max{F(i-1, v-kC(i)) + kW(i)}，其中0 <= kC(i) <= v 322.零钱兑换 F(i,v)=min_i{F(i,v), F(i-1,v-C(i))+1}

数学 Math

常用python中的数学操作：

操作 代码
乘方 pow(4,3) 和 4 ** 3 都表示4的3次方
平方根 math.sqrt(25) 和 pow(25, 0.5) 都表示对25求平方根
最大公约数 math.gcd(a, b)表示求a和 b的最大公约数（辗转取余）

计算

质数

拒绝采样

几何

排列组合

卡特兰数

卡特兰数$C_n$满足以下递推关系：

卡特兰数$C_n$满足以下递推关系$C_{n+1} = C_0C_n+C_1C_{n-1}+…+C_nC_0 = \sum_{i=0}^n C_iC_{n-i}$

统计

最大数

众数

出现次数超过列表长度一半的数。

中位数

中位数是有序列表中间的数。

特性：中位数可以将有序列表分成左右长度相同的两个子列表。

平均值

扫描线算法 Line Sweep

扫描线（面）算法来自计算机图形学，原本用于多边形的填充显示。使用虚拟扫描线可以来解决欧几里德空间中的各种几何问题。

推荐阅读：

典型题

脑筋急转弯

此类题通常需要找规律。

多线程

常用操作：

1
2
3
4
5
6
7
from threading import Lock

l = Lock()  # 初始化一个锁
l.acquire()  # 等待获取锁，并锁定
l.release()  # 释放该锁
with l:   # 获取锁；执行动作；释放锁
    xxx

典型题

刷题推荐阅读资料