深度生成模型总结--原始GAN和VAE

前段时间研究了一段Zero Shot Learning，研究了一些生成模型，总结一下备忘。

关于生成模型有一个很好的github仓库，而且作者的博客写的也非常精彩。

所谓生成模型，即，给定一些数据，用一个向量$x$表示，每一个datapoint对应一张图片或者一句话，生成模型的目标是学会$P(x)$，有了$P(x)$就可以从中sample，从而生成一些数据。

本文主要总结下GAN和VAE两种生成模型。

GAN

简介

GAN的原始paper是大神Goodfellow的《Generative Adversarial Nets》

先简介下模型的思想：

GAN包含：一个生成模型$G$和一个判别模型$D$，$G$的输入是一个随机扰动$z$，输出是生成的数据$\hat x$；$D$的输入是原始数据$x$或者$G$生成的数据$\hat x$，输出是输入来自训练数据的概率。

如果将$G$看作假币生产者，$D$看作警察，那么作假者的任务是尽量生产可以以假换真的假币，警察的任务是尽可能区分假币和真币，二者将不断地竞争直到生产者生产的假币完全以假乱真。

目标函数

$$\underset{G}{min}\underset{D}{max};V(D, G) = E_{x∼p_{data}(x)}[log
D(x)] + E_{z∼p_z(z)}[log(1 − D(G(z)))]$$

上面的目标函数修改自交叉熵损失函数。

算法流程

很多初次接触GAN的同学都会对GAN的训练感到迷惑，看下面的训练算法：

• 每轮训练迭代：
  • 前k步，训练分类器：
    • 从先验噪声：$p_g(z)$中采样m个噪声作为minibatch：${z^{(1)}, …, z^{(m)}}$。
    • 从数据生成分布中$p_{data}(x)$采样m个真实数据作为minibatch：${x^{(1)}, …, x^{(m)}}$。
• 使用随机梯度上升更新判别器的参数：
  • $\bigtriangledown_{\theta_d}\frac{1}{m}\sum_{i=1}^m[logD(x^{(i)})+log(D(G(z^{(i)})))]$
  • 从先验噪声：$p_g(z)$中采样m个噪声作为minibatch：${z^{(1)}, …, z^{(m)}}$。
  • 使用随机梯度下降更新生成器的参数：
    • $\bigtriangledown_{\theta_g}\frac{1}{m}\sum_{i=1}^mlog(D(G(z^{(i)})))$

虽然是同一个损失函数按照相反的方向训练，但训练判别器和生成器时针对的参数不同（上面算法中$\theta_d$和$\theta_g$），因此并不会出现南辕北辙的情况。

优缺点

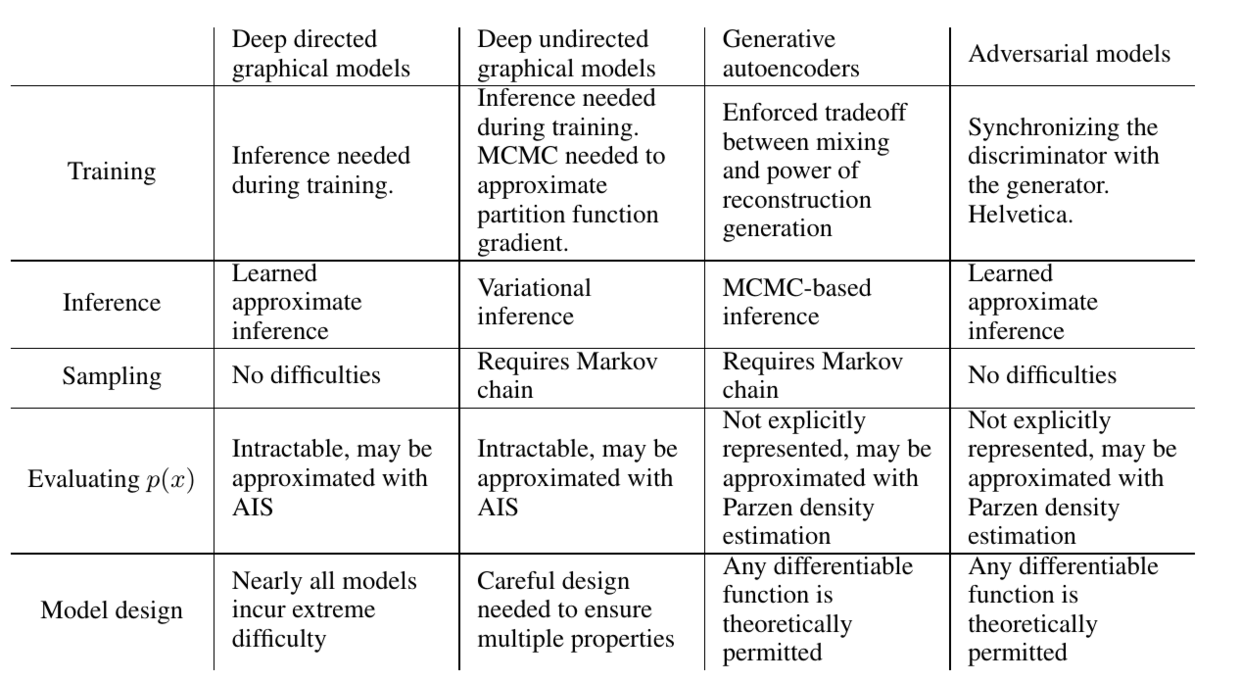
• 缺点：没有明确的$p_g(x)$的表示；$D$的训练需要和$G$同步。
• 优点：采样时无需Markov chain；训练时无需inference，模型设计的范围更广。

代码

下面代码来自https://github.com/wiseodd/generative-models ，使用python3.5。

%matplotlib inline
import torch
import torch.nn.functional as nn
import torch.autograd as autograd
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import os
from torch.autograd import Variable
from tensorflow.examples.tutorials.mnist import input_data


mnist = input_data.read_data_sets('data', one_hot=True)
mb_size = 64
Z_dim = 100
X_dim = mnist.train.images.shape[1]
y_dim = mnist.train.labels.shape[1]
h_dim = 128
c = 0
lr = 1e-3


def xavier_init(size):
    in_dim = size[0]
    xavier_stddev = 1. / np.sqrt(in_dim / 2.)
    return Variable(torch.randn(*size) * xavier_stddev, requires_grad=True)


""" ==================== GENERATOR ======================== """

Wzh = xavier_init(size=[Z_dim, h_dim])
bzh = Variable(torch.zeros(h_dim), requires_grad=True)

Whx = xavier_init(size=[h_dim, X_dim])
bhx = Variable(torch.zeros(X_dim), requires_grad=True)


def G(z):
    """一个简单的双层神经网络作为生成器"""
    h = nn.relu(z @ Wzh + bzh.repeat(z.size(0), 1))  # @是python3中新加入的矩阵乘法符号
    X = nn.sigmoid(h @ Whx + bhx.repeat(h.size(0), 1))
    return X


""" ==================== DISCRIMINATOR ======================== """

Wxh = xavier_init(size=[X_dim, h_dim])
bxh = Variable(torch.zeros(h_dim), requires_grad=True)

Why = xavier_init(size=[h_dim, 1])
bhy = Variable(torch.zeros(1), requires_grad=True)


def D(X):
    """一个简单的双层神经网络作为生成器"""
    h = nn.relu(X @ Wxh + bxh.repeat(X.size(0), 1))
    y = nn.sigmoid(h @ Why + bhy.repeat(h.size(0), 1))
    return y


G_params = [Wzh, bzh, Whx, bhx]
D_params = [Wxh, bxh, Why, bhy]
params = G_params + D_params


""" ===================== TRAINING ======================== """


def reset_grad():
    for p in params:
        if p.grad is not None:
            data = p.grad.data
            p.grad = Variable(data.new().resize_as_(data).zero_())

# 优化器指定参数
G_solver = optim.Adam(G_params, lr=1e-3)
D_solver = optim.Adam(D_params, lr=1e-3)

ones_label = Variable(torch.ones(mb_size))
zeros_label = Variable(torch.zeros(mb_size))


for it in range(10000):
    # Sample data
    z = Variable(torch.randn(mb_size, Z_dim))
    X, _ = mnist.train.next_batch(mb_size)
    X = Variable(torch.from_numpy(X))

    # Dicriminator forward-loss-backward-update
    G_sample = G(z)
    D_real = D(X)
    D_fake = D(G_sample)

    D_loss_real = nn.binary_cross_entropy(D_real, ones_label)
    D_loss_fake = nn.binary_cross_entropy(D_fake, zeros_label)
    D_loss = D_loss_real + D_loss_fake

    D_loss.backward()
    D_solver.step()

    # Housekeeping - reset gradient
    reset_grad()

    # Generator forward-loss-backward-update
    z = Variable(torch.randn(mb_size, Z_dim))
    G_sample = G(z)
    D_fake = D(G_sample)

    G_loss = nn.binary_cross_entropy(D_fake, ones_label)

    G_loss.backward()
    G_solver.step()

    # Housekeeping - reset gradient
    reset_grad()

    # Print and plot every now and then
    if it % 1000 == 0:
        print('Iter-{}; D_loss: {}; G_loss: {}'.format(it, D_loss.data.numpy(), G_loss.data.numpy()))

        # 取前16张图保存
        samples = G(z).data.numpy()[:16]

        fig = plt.figure(figsize=(4, 4))
        gs = gridspec.GridSpec(4, 4)
        gs.update(wspace=0.05, hspace=0.05)

        for i, sample in enumerate(samples):
            ax = plt.subplot(gs[i])
            plt.axis('off')
            ax.set_xticklabels([])
            ax.set_yticklabels([])
            ax.set_aspect('equal')
            plt.imshow(sample.reshape(28, 28), cmap='Greys_r')

        if not os.path.exists('out/'):
            os.makedirs('out/')

        plt.savefig('out/{}.png'.format(str(c).zfill(3)), bbox_inches='tight')
        c += 1
        plt.close(fig)

Extracting data/train-images-idx3-ubyte.gz
Extracting data/train-labels-idx1-ubyte.gz
Extracting data/t10k-images-idx3-ubyte.gz
Extracting data/t10k-labels-idx1-ubyte.gz

Iter-0; D_loss: [ 1.50280118]; G_loss: [ 1.64008629]
Iter-1000; D_loss: [ 0.0023118]; G_loss: [ 8.38419437]
Iter-2000; D_loss: [ 0.00522094]; G_loss: [ 7.93807125]
Iter-3000; D_loss: [ 0.03023708]; G_loss: [ 4.29144192]
Iter-4000; D_loss: [ 0.02870584]; G_loss: [ 6.23502254]
Iter-5000; D_loss: [ 0.15886861]; G_loss: [ 4.66118479]
Iter-6000; D_loss: [ 0.26347995]; G_loss: [ 4.20204782]
Iter-7000; D_loss: [ 0.51319796]; G_loss: [ 2.98293495]
Iter-8000; D_loss: [ 0.70317507]; G_loss: [ 2.42791796]
Iter-9000; D_loss: [ 0.93306208]; G_loss: [ 2.59884763]

生成效果

VAE

简介

关于VAE可以直接看这篇《Tutorial on Variational Autoencoders》。

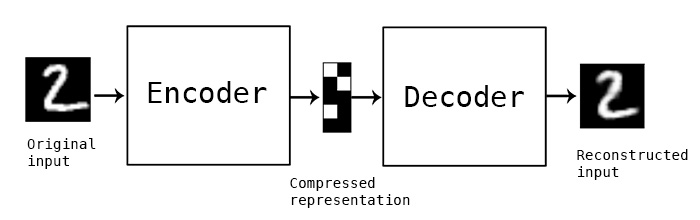
先来看看普通的Auto-Encoder长什么样：

也就是$x$作为输入，要努力使输出$\tilde x$接近$x$，最终使用的是中间的隐层向量，作为一个输入$x$的特征。

VAE是结合了隐变量（latent variable）的Auto-Encoder。

先考虑隐变量，假设输入的是一张猫的图片，隐变量可以是“腿的个数”/“耳朵的大小”等。

那么原来的生成模型可以转换成：$P(X) = \int P(X \vert z) P(z) dz$，$z$是隐变量（向量）。

但是手动去设计$z$向量显然是不可操作的，于是VAE假设，$z$的某个维度并不能简单地解释，并且$z\sim N(0,I)$。即便有这样的先验假设，只要映射函数足够复杂（$P(X|z)$），最终的$P(X)$也可以足够复杂。

但是这里还有一个问题，即，对于大多数的$z$，$P(X|z)=0$，直接去做积分是一个很没有必要的劳动。

于是有人提出，学一个$Q(z|X)$，这个$Q$可以根据某个$X$，返回可能的$z$的分布。我们希望这里的$z$是比较可能产生$X$的，即$P(X|z)>0$，并且这里的$z$的空间比一开始$z$的空间要小。这样的话，计算$E_{z\sim Q}P(X|z)$去代替上面的积分，会更简单。

下面计算$Q(z|X)$和$P(z|X)$的KL散度：

$$D_{KL}[Q(z \vert X)
\Vert P(z \vert X)] = \sum_z Q(z \vert X) , \log \frac{Q(z \vert X)}{P(z \vert
X)} $$
$$= E_{z\sim Q} \left[ \log \frac{Q(z \vert
X)}{P(z \vert X)} \right]$$
$$= E_{z\sim Q}[\log Q(z
\vert X) - \log P(z \vert X)]$$
$$= E_{z\sim Q} \left[
\log Q(z \vert X) - \log \frac{P(X \vert z) P(z)}{P(X)} \right]$$
$$= E_{z\sim Q}[\log Q(z \vert X) - (\log P(X \vert z) + \log P(z) - \log P(X))]$$
$$= E_{z\sim Q}[\log Q(z \vert X) - \log P(X \vert z) - \log P(z) + \log P(X)]$$

把$\log P(X)$移到左边：

$$\log P(X) - D_{KL}[Q(z \vert
X) \Vert P(z \vert X)] $$
$$= E_{z\sim Q}[\log P(X \vert z) - (\log Q(z \vert X) - \log P(z))]$$
$$= E_{z\sim Q}[\log P(X \vert z)] - E[\log Q(z \vert X) - \log P(z)] $$
$$= E_{z\sim Q}[\log P(X \vert z)] - D_{KL}[Q(z \vert X) \Vert P(z)]$$

于是我们得到了VAE的核心方程（目标函数）：

$$\log P(X) - D_{KL}[Q(z \vert X) \Vert P(z \vert X)]$$
$$= E_{z\sim Q}[\log P(X \vert z)] - D_{KL}[Q(z \vert X) \Vert P(z)]$$

等式的左边：

1. $\log P(X)$是对数似然函数，使我们要最大化的对象；
2. $- D_{KL}[Q(z \vert X) \Vert P(z \vert X)]$，使用$Q(z \vert X)$代替$ P(z \vert X)$时的产生的误差项。于是左边可以理解成：我们要找一个$\log P(X)$的下界函数。

回顾下一开始介绍的Auto-Encoder，我们可以：

• 把$Q(z \vert X)$当做Encoder；
• 把z当做隐层；
• 把$P(X \vert z)$当做Decoder。
  等式的右边：这部分是我们可以用随机梯度下降去优化的。

1. $E_{z\sim Q}[\log P(X \vert z)]$是Decoder的目标函数，即如果把z理解成输入，X是输出，则$E_{z\sim Q}[\log P(X \vert z)]$是极大似然函数；
2. $-D_{KL}[Q(z \vert X) \Vert P(z)]$是Encoder的目标函数，要训练一个使$Q(z \vert X)$尽可能接近$P(z)$的Encoder。

之前我们已经限定$z\sim N(0, I)$，现在再限定$Q(z \vert X)$服从参数是$\mu(X)$和$\Sigma(X)$的高斯分布。这时，右边第二项是有准确表达式的：

$$D_{KL}[N(\mu(X),\Sigma(X)) \Vert N(0, 1)] = \frac{1}{2} \sum_k \left( \exp(\Sigma(X)) + \mu^2(X) - 1 - \Sigma(X) \right)$$

至于右边第一个表达式，我们可以使用二次损失函数替代。

这里为了训练的方便，使用了重参数技巧（reparameterization trick），即，引入一个随机性变量：$\epsilon \sim N(0,1)$，$z = \mu(X) + \Sigma^{\frac{1}{2}}(X) , \epsilon$，这样使得网络反向传播时没有涉及到随机变量。

代码

import torch
import torch.nn.functional as nn
import torch.autograd as autograd
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import os
from torch.autograd import Variable
from tensorflow.examples.tutorials.mnist import input_data


mnist = input_data.read_data_sets('data', one_hot=True)
mb_size = 64
Z_dim = 100
X_dim = mnist.train.images.shape[1]
y_dim = mnist.train.labels.shape[1]
h_dim = 128
c = 0
lr = 1e-3


def xavier_init(size):
    in_dim = size[0]
    xavier_stddev = 1. / np.sqrt(in_dim / 2.)
    return Variable(torch.randn(*size) * xavier_stddev, requires_grad=True)


# =============================== Q(z|X) ======================================

Wxh = xavier_init(size=[X_dim, h_dim])
bxh = Variable(torch.zeros(h_dim), requires_grad=True)

Whz_mu = xavier_init(size=[h_dim, Z_dim])
bhz_mu = Variable(torch.zeros(Z_dim), requires_grad=True)

Whz_var = xavier_init(size=[h_dim, Z_dim])
bhz_var = Variable(torch.zeros(Z_dim), requires_grad=True)


def Q(X):
    h = nn.relu(X @ Wxh + bxh.repeat(X.size(0), 1))
    z_mu = h @ Whz_mu + bhz_mu.repeat(h.size(0), 1)
    z_var = h @ Whz_var + bhz_var.repeat(h.size(0), 1)
    return z_mu, z_var


def sample_z(mu, log_var):
    eps = Variable(torch.randn(mb_size, Z_dim))
    return mu + torch.exp(log_var / 2) * eps


# =============================== P(X|z) ======================================

Wzh = xavier_init(size=[Z_dim, h_dim])
bzh = Variable(torch.zeros(h_dim), requires_grad=True)

Whx = xavier_init(size=[h_dim, X_dim])
bhx = Variable(torch.zeros(X_dim), requires_grad=True)


def P(z):
    h = nn.relu(z @ Wzh + bzh.repeat(z.size(0), 1))
    X = nn.sigmoid(h @ Whx + bhx.repeat(h.size(0), 1))
    return X


# =============================== TRAINING ====================================

params = [Wxh, bxh, Whz_mu, bhz_mu, Whz_var, bhz_var,
          Wzh, bzh, Whx, bhx]

solver = optim.Adam(params, lr=lr)

for it in range(10000):
    X, _ = mnist.train.next_batch(mb_size)
    X = Variable(torch.from_numpy(X))

    # Forward
    z_mu, z_var = Q(X)
    z = sample_z(z_mu, z_var)
    X_sample = P(z)

    # Loss
    recon_loss = nn.binary_cross_entropy(X_sample, X, size_average=False) / mb_size
    kl_loss = torch.mean(0.5 * torch.sum(torch.exp(z_var) + z_mu**2 - 1. - z_var, 1))
    # loss包含两项：重构损失（Decoder），kl损失（Encoder）
    loss = recon_loss + kl_loss

    # Backward
    loss.backward()

    # Update
    solver.step()

    # Housekeeping
    for p in params:
        if p.grad is not None:
            data = p.grad.data
            p.grad = Variable(data.new().resize_as_(data).zero_())

    # Print and plot every now and then
    if it % 1000 == 0:
        print('Iter-{}; Loss: {:.4}'.format(it, loss.data[0]))

        samples = P(z).data.numpy()[:16]

        fig = plt.figure(figsize=(4, 4))
        gs = gridspec.GridSpec(4, 4)
        gs.update(wspace=0.05, hspace=0.05)

        for i, sample in enumerate(samples):
            ax = plt.subplot(gs[i])
            plt.axis('off')
            ax.set_xticklabels([])
            ax.set_yticklabels([])
            ax.set_aspect('equal')
            plt.imshow(sample.reshape(28, 28), cmap='Greys_r')

        if not os.path.exists('out/'):
            os.makedirs('out/')

        plt.savefig('out/{}_vae.png'.format(str(c).zfill(3)), bbox_inches='tight')
        c += 1
        plt.close(fig)

Extracting data/train-images-idx3-ubyte.gz
Extracting data/train-labels-idx1-ubyte.gz
Extracting data/t10k-images-idx3-ubyte.gz
Extracting data/t10k-labels-idx1-ubyte.gz
Iter-0; Loss: 790.1
Iter-1000; Loss: 157.6
Iter-2000; Loss: 132.7
Iter-3000; Loss: 121.2
Iter-4000; Loss: 118.5
Iter-5000; Loss: 115.5
Iter-6000; Loss: 118.2
Iter-7000; Loss: 114.2
Iter-8000; Loss: 108.9
Iter-9000; Loss: 108.6

生成效果