18. Confronting the Partition Function
配分函数(Partition Function)
许多概率模型(通常是无向图模型)由一个未归一化的概率分布$\tilde{p}(x,θ)$定义。
必须通过除以配分函数Z(θ)来归一化$\tilde{p}$,以获得一个有效的概率分布:$p(x;θ)=\frac{1}{Z(θ)}\tilde{p}(x;θ)$。
配分函数是未归一化概率所有状态的积分(对于连续变量)或求和(对于离散变量):$∫\tilde{p}(x)dx$或者$∑_x\tilde{p}(x)$。对很多有趣的模型,以上积分或求和难以计算。
有些深度学习模型被设计成具有一个易于处理的归一化常数,或被设计成能够在不涉及计算p(x)p(x)的情况下使用。
然而,其他一些模型会直接面对难以计算的配分函数的挑战。
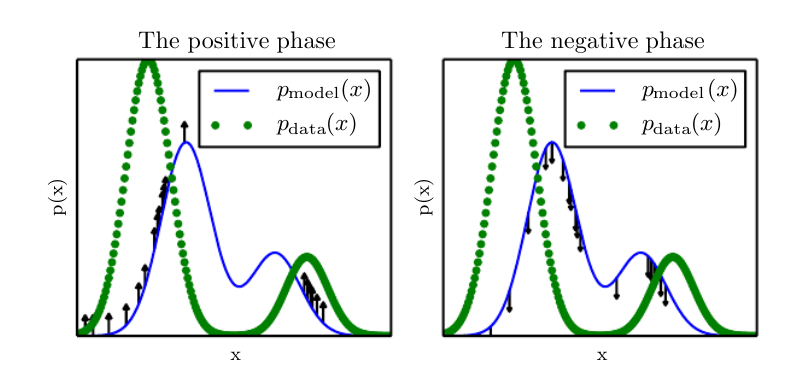
对数似然梯度(Log-Likelihood Gradient):对数似然对参数的梯度具有一项对应于配分函数的梯度:$∇_θlogp(x;θ)=∇_θlog\tilde{p}(x;θ)−∇_θlogZ(θ)$,这是非常著名的正相(positive phase)和负相(negative phase)的分解。
对于保证所有的$x$都有$p(x)>0$的模型,我们可以用$exp(log\tilde{p}(x))$代替$\tilde{p}(x)$,$∇_θlogZ(θ)$可以化简成$E_{x\sim p(x)}∇_θlog\tilde{p}(x)$。 转换成这种形式后,我们自然可以考虑用蒙特卡洛法来近似这个期望。
在正相中,我们增大从数据中采样得到的$log\tilde{p}(x)$。
在负相中,我们通过降低从模型分布中采样的$log\tilde{p}(x)$来降低配分函数。
基于MCMC的方法
朴素的MCMC算法:该算法计算代价太高,实际上不可行。 但是是其他算法的思想基础。

负相涉及到从模型分布中抽样,可以认为它在找模型信任度很高的点。 负相减少了这些点的概率,这些点一般被认为代表了模型不正确的信念。
还可以用“做梦”来帮助理解:我们的大脑维护了一个现实世界的概率模型。醒着的时候,当你经历真实的事件,相当于按照$\tilde{p}(x)$的梯度去完善这个模型;做梦相当于从这个概率模型里随机抽样,当你醒来发现这是梦,就会按照$\tilde{p}(x)$的负梯度去更新模型,因为你知道梦是假的。
对比散度(Contrastive Divergence,CD)算法:接下来寻找计算代价更低的替代算法。
朴素的MCMC算法的计算成本主要来自每一步的随机初始化磨合马尔可夫链。
一个自然的解决方法是初始化马尔可夫链为一个非常接近模型分布的分布,从而大大减少磨合步骤。 CD算法在每个步骤中初始化马尔可夫链为采样自数据分布中的样本。
缺点:它不能抑制远离真实训练样本的高概率区域。 这些区域在模型上具有高概率,但是在数据生成区域上具有低概率,被称为虚假模态(spurious modes)。
在训练诸如RBM的浅层网络时,CD算法是很有用的;但CD算法并不直接有助于训练更深的模型。

持续性对比散度(Persistent Contrastive Divergence,PCD)算法:又称随机最大似然(Stochastic Maximum Likelihood,SML),不同于CD,它在每个梯度步骤中初始化马尔可夫链为先前梯度步骤的状态值。
因为每个马尔可夫链在整个学习过程中不断更新,而不是在每个梯度步骤中重新开始,马尔可夫链可以自由探索很远,以找到模型的所有峰值。
因此,SML比CD更不容易形成具有虚假模态的模型。

伪似然(Pseudolikelihood):伪似然基于以下观察:无向概率模型中很容易计算概率的比率:$\frac{p(x)}{p(y)}=\frac{\frac{1}{Z}\tilde{p}(x)}{\frac{1}{Z}\tilde{p}(y)}=\frac{\tilde{p}(x)}{\tilde{p}(y)}$。伪似然的目标函数使用条件概率:$∑_{i=1}^nlogp(x_i∣x_{−i})$。
如果每个随机变量有k个不同的值,那么考虑边缘概率的计算,$\tilde{p}$需要$k×n$次估计,而计算配分函数需要$k^n$次估计。
得分匹配(Score Matching):对数密度关于参数的导数$∇_xlogp(x)$,被称为其得分(Score)。
$$L(x, \theta) = \frac{1}{2} || ∇_x \log p_{model}(x; \theta) - ∇_x log p_{data} (x) ||_2^2$$
用下面的式子估计:
$$ \tilde{L}(x,\theta)=\sum_{j=1}^n(\frac{\partial^2}{\partial x^2_j}logp_{model}(x;\theta)+\frac{1}{2}(\frac{\partial }{\partial x_j}logp_{model}(x;\theta))^2 )$$
比率匹配(Ratio Matching):比率匹配特别适用于二值数据。
比率匹配最小化以下目标函数在样本上的均值:
$$L^{(RM)}(x,θ)=∑_{j=1}{n}(\frac{1}{1+\frac{p_{model}(x;θ)}{p_{model}(f(x),j;θ)}}^2$$
其中f(x,j)返回j处位值取反的x。
比率匹配使用了与伪似然估计相同的策略来绕开配分函数:配分函数会在两个概率的比率中抵消掉。
去噪得分匹配(Denoising Score Matching):可以去拟合正则化的$p_{smoothed}(x)=∫p_{data}(y)q(x∣y)dy$,而不是拟合真实分布$p_{data}$。
分布q(x∣y)是一个损坏过程,通常在形成x的过程中会向y中添加少量噪声。
噪声对比估计(Noise-Contrastive Estimation,NCE):噪声对比估计直接估计模型的概率分布:$\log p_{model} (x) = \log \tilde{p}_{model} (x; \theta) + c$,其中c是$−logZ(θ)$的近似。 噪声对比估计过程将c视为另一参数,使用相同的算法同时估计θ和c。
NCE将估计p(x)的无监督学习问题转化为学习一个概率二元分类器,其中一个类别对应模型生成的数据,另一个对应噪声生成的数据。
具体地:我们引入噪声分布$p_{noise}(x)$。 噪声分布应该易于估计和从中采样。 再构造一个联合x和新二值变量y的模型。
指定:$p_{joint}(y=1)=\frac{1}{2}$,有$p_{joint}(x∣y=1)=p_{model}(x)$和$p_{joint}(x∣y=0)=p_{noise}(x)$
直接估计配分函数:当我们需要评估模型,监控训练性能,和比较模型时,还是需要直接估计配分函数,我们可以考虑蒙塔卡洛的方法去估计它。
首先找到一个简单的提议分布(proposal distribution):$p_0(x)=\frac{1}{Z_0}\tilde{p}_0(x)$,其在配分函数$Z_0$和未归一化分布$\tilde{p}_0(x)$上易于采样和估计。
那么:
$$Z_1=∫\tilde{p}_1(x)dx=∫\frac{p_0(x)}{p_0(x)}\tilde{p}_1(x)dx=Z_0∫p_0(x)\frac{\tilde{p}_1(x)}{\tilde{p}_0(x)dx}$$
可以使用简单重要采样(importance sampling)来估计:
$$\hat{Z}_1=\frac{Z_0}{K}\sum_{k=1}^K\frac{\tilde{p}_1(x^{(k)})}{\tilde{p}_0(x^{(k)})};;s.t.;:;x^{(k)}\sim p_0$$
退火重要采样(Annealed Importance Sampling, AIS):在$D_{KL}(p_0|p_1)$很大的情况下(即$p_0$和$p_1$之间几乎没有重叠),退火重要采样通过引入中间分布来缩小这种差距。
考虑分布序列$p_{η_0},…,p_{η_n}$,其中$0=η_0<η_1<⋯<η_{n−1}<η_n=1$,分布序列中的第一个和最后一个分别是p0和p1。
$\frac{Z_1}{Z_0}$写作$\frac{Z_1}{Z_0}=\prod_{j=0}^{n-1} \frac{Z_{η_{j+1}}}{Z_{η_j}}$。
如果对于所有的$0≤j≤n−10≤j≤n−1$,分布$p_{η_j}$和$p_{η_{j+1}}$足够接近,那么能够使用简单的重要采样来估计每个因子$\frac{Z_{η_{j+1}}}{Z_{η_j}}$,然后使用这些得到$\frac{Z_1}{Z_0}$的估计。
中间分布的一个通用和流行选择是使用目标分布p1和建议分布p0的加权几何平均:$p_{η_j}∝p^{η_j}_1p^{1−η_j}_0$。
桥式采样(Bridge Sampling):桥式采样依赖于单个分布$p^∗$(被称为桥),在已知配分函数的分布$p_0$和分布$p_1$之间插值。
$$\frac{Z_1}{Z_0} ≈ \frac{\sum_{k=1}^K \frac{ \tilde{p}(x_0^{(k)}) }{\tilde{p}_0(x_0^{(k)}) }} {\sum_{k=1}^K \frac{ \tilde{p}(x_1^{(k)}) }{\tilde{p}_1(x_1^{(k)}) }} $$
最优的桥式采样是$p^{(opt)}_∗(x)∝\frac{\tilde{p}_0(x)\tilde{p}_1(x)}{r\tilde{p}_0(x)+\tilde{p}_1(x)}$,其中$r=Z_1/Z_0$。可以从粗糙的r开始估计,然后使用得到的桥式采样逐步迭代以改进估计。