20. Deep Generative Models

玻尔兹曼机（Boltzmann Machines）

我们在d维二值随机向量$x∈{0,1}^d$上定义玻尔兹曼机：

玻尔兹曼机是一种基于能量的模型，意味着我们可以使用能量函数定义联合概率分布：
$P(x) = \frac{\exp(-E(x))}{Z}$，其中$E(x)$是能量函数，Z是确保$∑_xP(x)=1$的配分函数。
玻尔兹曼机的能量函数如下给出： $E(x) = -x^TUx - b^Tx$，其中$U$是模型参数的“权重”矩阵，$b$是偏置向量。
带隐变量的玻尔兹曼机：$E(v,h)=−v^⊤Rv−v^⊤Wh−h^⊤Sh−b^⊤v−c^⊤h$。

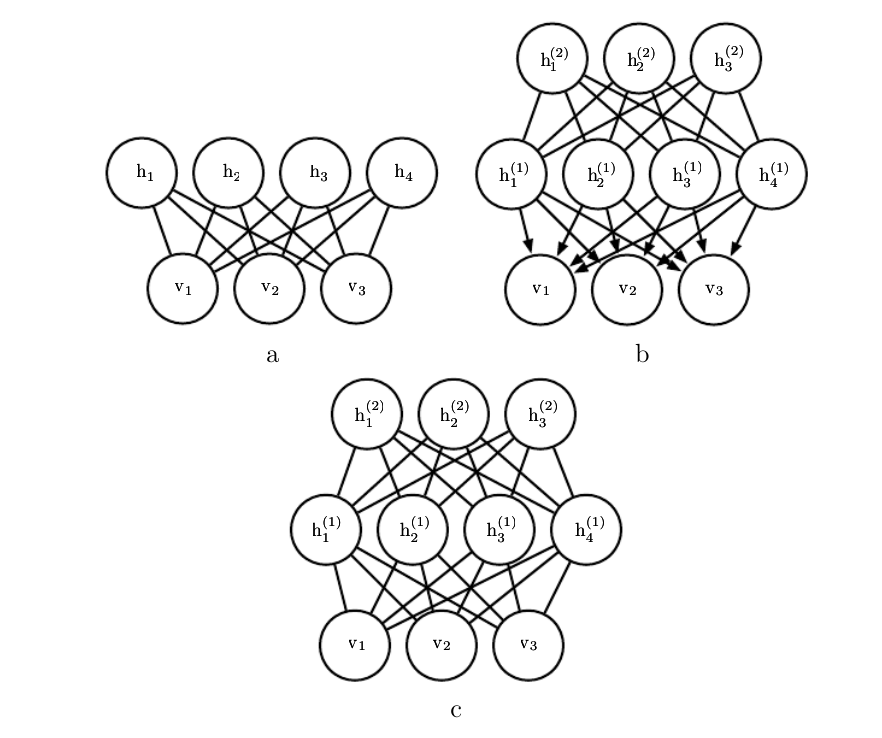
a是受限玻尔兹曼机，RBM；b是深度信念网络，DBN；c是深度玻尔兹曼机，DBM。

Hebbian学习规则

我们可以假定，反射活动的持续与重复会导致神经元稳定性的持久性提升。
当神经元A的轴突与神经元B很近并参与了对B的重复持续的兴奋时，这两个神经元或其中一个便会发生某些生长过程或代谢变化，致使A作为能使B兴奋的细胞之一，它的效能增强了。
这一理论经常会被总结为“一起激发的神经元连在一起”（Cells that fire together, wire
together）。这段摘自wikipedia。

受限玻尔兹曼机（Restricted Boltzmann Machine）

其能量函数为：$E(v,h)=−b^⊤v−c^⊤h−v^⊤Wh$，“受限”在于同层之间没有连接。

使用训练具有难以计算配分函数的模型的技术来训练RBM。
这包括CD,SML（PCD）,比率匹配等。

与深度学习中使用的其他无向模型相比，因为我们可以以闭解形式计算P(h∣v)，RBM可以相对直接地训练。

深度信念网络（Deep Belief Networks）

目前使用较少，但历史地位突出。特点：顶部两层之间的连接是无向的。
而所有其他层之间的连接是有向的，箭头指向最接近数据的层。

一个具有l个隐藏层的DBN包含l个权重矩阵：$W^{(1)},…,W^{(l)}$。

同时也包含l+1个偏置向量： $b^{(0)},…,b^{(l)}$，其中$b^{(0)}$是可见层的偏置。

DBN表示的概率分布由下式给出：

$$P(h^{(l)}, h^{(l-1)}) ∝ exp ( b^{(l)^T}h^{(l)}+ b^{(l-1)^T}h^{(l-1)}+h^{(l-1)^T}W^{(l)}h^{(l)} )$$

$$P(h_i^{(k)} = 1 | h^{(k+1)}) = \sigma ( b_i^{(k)} + W_{:,i}^{(k+1)^T}h^{(k+1)} )~ \forall i,
\forall k \in 1, …, l-2$$

$$P(v_i = 1 | h^{(1)}) = \sigma ( b_i^{(0)} +
W_{:,i}^{(1)^T}h^{(1)})~ \forall i $$

在实值可见单元的情况下，替换$v∼N(v;b(0)+W(1)^⊤h(1),β−1)$。

采样：先在顶部的两个隐藏层上运行几个Gibbs采样；再对后面的有向图进行ancestral采样。

深度玻尔兹曼机（Deep Boltzmann Machines）

特点：与DBN不同的是，它是一个完全无向的模型；与RBM不同的是，它有几层潜变量（RBM只有一层）。
在一个深度玻尔兹曼机包含一个可见层v和三个隐藏层$h^{(1)},h^{(2)}和h^{(3)}$（$h^{(1)}$最靠近底层的可见层）的情况下，联合概率由下式给出

$$P(v,h^{(1)},h^{(2)},h^{(3)})=\frac{1}{Z(θ)}exp(−E(v,h^{(1)},h^{(2)},h^{(3)};θ))$$

能量函数：

$$E(v, h^{(1)},h^{(2)},h^{(3)}; \theta) = -v^⊤
W^{(1)}h^{(1)}-h^{(1)⊤}W^{(2)}h^{(2)}- h^{(2)⊤}W^{(3)}h^{(3)}$$

条件概率：

$$P(v_i=1|h^{(1)})=σ(W_{i,:}^{(1)})$$

$$P(h_i^{(1)}|v,h^{(2)})=σ(v^⊤W_{:,i}^{(1)}+W_{i,:}^{(2)}h^{(2)})$$

$$P(h_k^{(2)}=1|h^{(1)})=σ(h^{(1)T}W_{:,k}^{(2)})$$

二分图结构使Gibbs采样能在深度玻尔兹曼机中高效采样。

有趣的性质：使用适当的均匀场允许DBM的近似推断过程捕获自顶向下反馈相互作用的影响。

这从神经科学的角度来看是有趣的，人脑使用许多自上而下的反馈连接。

DBM的一个缺点是采样时所有层都要使用MCMC。

均匀场估计：对于两层隐层的DBM，令$Q(h^{(1)},h^{(2)}∣v)$为$P(h^{(1)},h^{(2)}∣v)$的近似。

均匀场假设意味着$Q(h^{(1)},h^{(2)}∣v)=∏_jQ(h^{(1)}_j∣v)∏_kQ(h^{(2)}_k∣v)$。

将Q作为Bernoulli分布的乘积进行参数化：对于每个j，有$\hat h^{(1)}_j=Q(h^{(1)}_j=1∣v)$,其中$\hat
h^{(1)}_j∈[0,1]$；

对于每个k，有$\hat h^{(2)}_k=Q(h^{(2)}_k=1∣v)$，其中$\hat h^{(2)}_k∈[0,1]$。

$Q(h^{(1)},h^{(2)}∣v)=∏_jQ(h^{(1)}_j∣v)∏_kQ(h^{(2)}_k∣v)$

$=∏_j(\hat h^{(1)}_j)^{h^{(1)}_j}(1−\hat h^{(1)}_j)^{(1−h^{(1)}_j)}×∏_k(\hat h^{(2)}_k)^{h^{(2)}_k}(1−\hat h^{(2)}_k)^{(1−h^{(2)}_k)}$。

更新规则：

$$\hat h_j^{(1)} = \sigma \Big( \sum_i v_i W_{i,j}^{(1)}+\sum_{k’}W_{j,k’}^{(2)} \hat
h_{k’}^{(2)} \Big), \forall j$$

$$\hat h_{k}^{(2)} = \sigma \Big( \sum_{j’}
W_{j’,k}^{(2)} \hat h_{j’}^{(1)} \Big), \forall k$$

参数学习：变分随机最大似然算法：

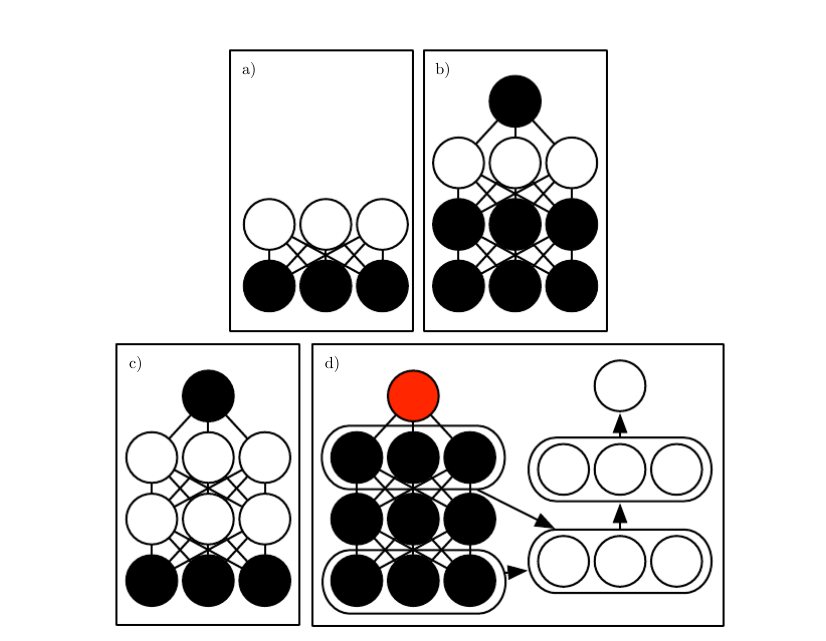
逐层预训练：用于分类MNIST的DBM的训练：

(a)使用CD近似最大化$\log P(v)$来训练RBM。
(b)训练第二个RBM，使用CD-k近似最大化$\log P(h^{(1)}, y)$来建模$h^{(1)}$和目标类$y$，其中$h^{(1)}$采自第一个RBM条件于数据的后验。在学习期间将$k$从$1$增加到$20$。
(c)将两个RBM组合为DBM。使用$k = 5$的随机最大似然训练，近似最大化$\log P(v,y)$。
(d)将$y$从模型中删除。定义新的一组特征$h^{(1)}$和$h^{(2)}$。使用随机梯度下降和Dropout训练MLP近似最大化$\log P(y|v)$。

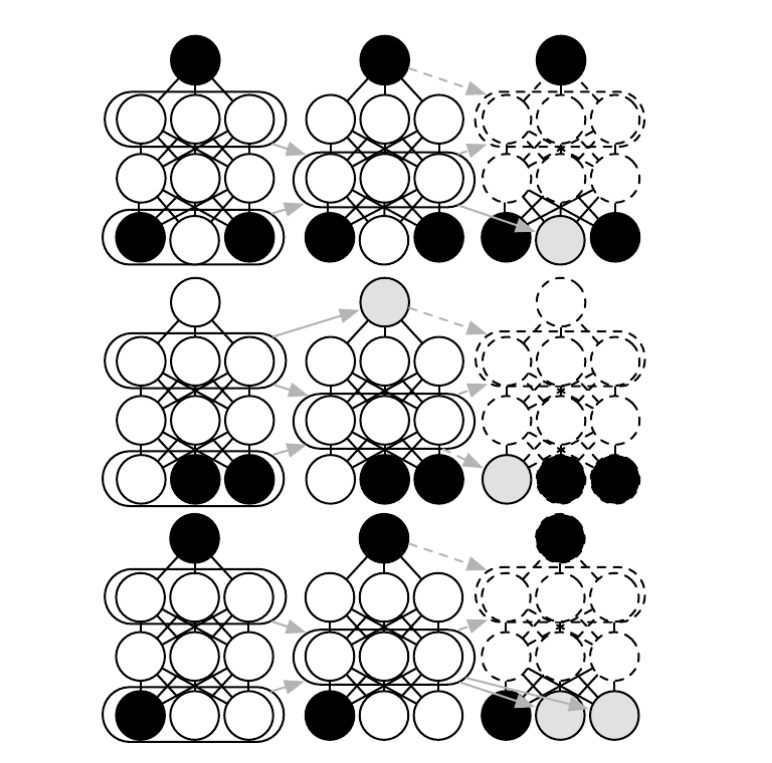
联合训练深度玻尔兹曼机：

实值数据上的玻尔兹曼机：

1.Gaussian-Bernoulli RBM

隐藏单元是二元的伯努利分布，可见单元上的条件分布是高斯分布（均值为隐藏单元的函数）。

条件分布：$p(v∣h)=N(v;Wh,β^{−1})$
能量函数的一种方式：$E(v,h)=\frac{1}{2}v^⊤(β⊙v)−(v⊙β)^⊤Wh−b^⊤h$。

2.均值和协方差RBM（Mean and Convariance RBM，mcRBM）

使用隐藏单元独立地编码所有可观察单元的条件均值和协方差。
mcRBM的隐藏层分为两组单元：均值单元和协方差单元。

在二值均值的单元h(m)和二值协方差单元h(c)的情况下，mcRBM模型被定义为两个能量函数的组合：

$$E_{mc}(x,h(m),h(c))=E_m(x,h(m))+E_c(x,h(c))$$

3.学生t分布均值乘积模型（Mean-Product of Student’s t-distribution）

隐藏变量的互补条件分布是由条件独立的Gamma分布给出。

能量函数为：

$$E_{mPoT}(x,h(m),h(c))=E_m(x,h^{(m)})+∑_j(h^{(c)}_j(1+\frac{1}{2}(r^{(j)T}x)^2)+(1−γ_j)logh^{(c)}_j)$$

4.尖峰和平板RBM（Spike and Slab RBM，ssRBM）

尖峰和平板RBM有两类隐藏单元：二值尖峰(spike)单元h和实值平板(slab)单元s。

条件于隐藏单元的可见单元均值由$(h⊙s)W^⊤$给出。
换句话说，每一列$W_{:,i}$定义当$h_i=1$时可出现在输入中的分量。

相应的尖峰变量$h_i$确定该分量是否存在。
如果存在的话，相应的平板变量$s_i$确定该分量的强度。

当尖峰变量激活时，相应的平板变量将沿着$W_{:,i}$定义的轴的输入增加方差。
这允许我们对输入的协方差建模。

通过随机操作的反向传播

传统的神经网络对一些输入变量$x$施加确定性变换；当开发生成模型时，我们经常希望扩展神经网络以实现$x$的随机变换。
这样做的一个直接方法是使用额外输入$z$来引入随机性。

函数$f(x,z)$对于不能访问z的观察者来说将是随机的。
如果f是连续可微的，我们可以像往常一样使用反向传播计算训练所需的梯度：$ω$是同时包含参数$θ$和输入$x$的变量，$y=f(z;ω)$，可以使用传统工具（例如反向传播算法）计算$y$相对于$ω$的导数。

至关重要的是：$ω$不能是$z$的函数，且$z$不能是$ω$的函数。

这种技术通常被称为重参数化技巧（reparametrization
trick）、随机反向传播(stochastic back-propagation)或扰动分析(perturbation analysis)。

通过离散随机操作的反向传播

REINFORCE算法（REward Increment = nonnegative Factor × Offset
Reinforcement × Characteristic Eligibility）提供了定义一系列简单而强大解决方案的框架。

其核心思想是:即使$J(f(z;ω))$是具有无用导数的阶跃函数，期望代价$E_{z\sim p(z)}J(f(z;ω))$通常是服从梯度下降的光滑函数。

$$E_z[J(y)]=∑_yJ(y)p(y)$$

$$\frac{∂E[J(y)]}{∂ω}=\sum_yJ(y)\frac{∂p(y)}{∂ω}=\sum_yJ(y)p(y)\frac{∂logp(y)}{∂ω}≈\frac{1}{m}∑^m_{y^{(i)}\sim p(y)},i=1$$

简单REINFORCE估计的一个问题是其具有非常高的方差，需要采y的许多样本才能获得对梯度的良好估计。
相对于$ω_i$的梯度估计则变为：

$$(J(y) - b(\omega)_i)\frac{\partial\log p(y)}{\partial \omega_i}$$

b的获取：

$$b^*(\omega)_i=\frac{E{p(y)} \Big[ J(y) \frac{\partial\log
p(y)^2}{\partial \omega_i} \Big]} {E_{p(y)} \Big[\frac{\partial\log
p(y)^2}{\partial \omega_i}\Big] }$$

有向生成网络：

sigmoid信念网络（Sigmoid Belief Nets）

将sigmoid信念网络视为具有二值向量的状态s，其中状态的每个元素都受其祖先影响：

$$p(s_i)=σ(\sum_{j< i}W_{j,i}s_j+b_i)$$

sigmoid信念网络最常见的结构是被分为许多层的结构，其中原始采样通过一系列多个隐藏层进行，然后最终生成可见层。

这种结构与深度信念网络非常相似，但它们在采样过程开始时的单元彼此独立，而不是从受限玻尔兹曼机采样。

可微生成器网络（Differentiable Generator Nets）

是很多生成模型的基础，使用可微函数$g(z;θ(g))$将潜变量z的样本变换为样本$x$或样本$x$上的分布，可微函数通常可以由神经网络表示。

给出x的训练样本，训练可微生成器网络的几种方法：

1.变分自编码器（Variational Autoencoders）

变分自编码器是一个使用学得近似推断（Learned Approximate Inference）的有向模型，
可以纯粹地使用基于梯度的方法进行训练。

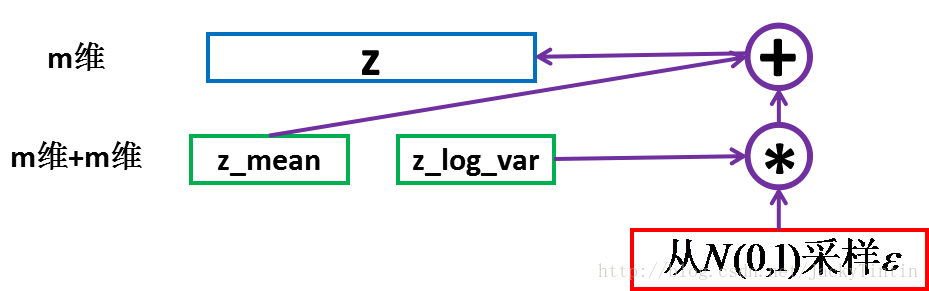
注：图片来自丁丁的博客。为了从模型生成样本，VAE首先从编码分布$p_{model}(z)$中采样$z$；

然后将样本输入到可微生成器网络
$g(z)$中；最后，从分布$p_{model}(x;g(z)) = p_{model}(x \mid z)$ 中采样$x$。
在训练期间，近似推断网络（或编码器）$q(z \mid x)$用于获得$z$，而$p_{model}(x \mid z)$则被视为解码器网络。
$log;p_{model}(x)\geq L(q)=E_{z\sim
q(z|x)}[log;p_{model}(x|z)]-D_{KL}(q(z|x)||p_{model}(z))$
变分自编码器方法是优雅的，易于实现的，也获得了不错的结果，是生成式建模中的最先进方法之一。
它的主要缺点是从在图像上训练的变分自编码器中采样的样本往往有些模糊。

2.生成式对抗网络（Generative Adversarial Networks）

生成器网络直接产生样本$x = g(z; theta^{(g)})$。

判别器网络试图区分从训练数据抽取的样本和从生成器抽取的样本。
$g^∗=arg;\underset{g}{min};\underset{d}{max};
v(g,d)$，$v$的默认选择是：$v(θ(g),θ(d))=E_{x\sim p_{data}}logd(x)+E_{x\sim
p_{model}}log(1−d(x))$。

设计GAN的主要动机是学习过程既不需要近似推断也不需要配分函数梯度的近似。

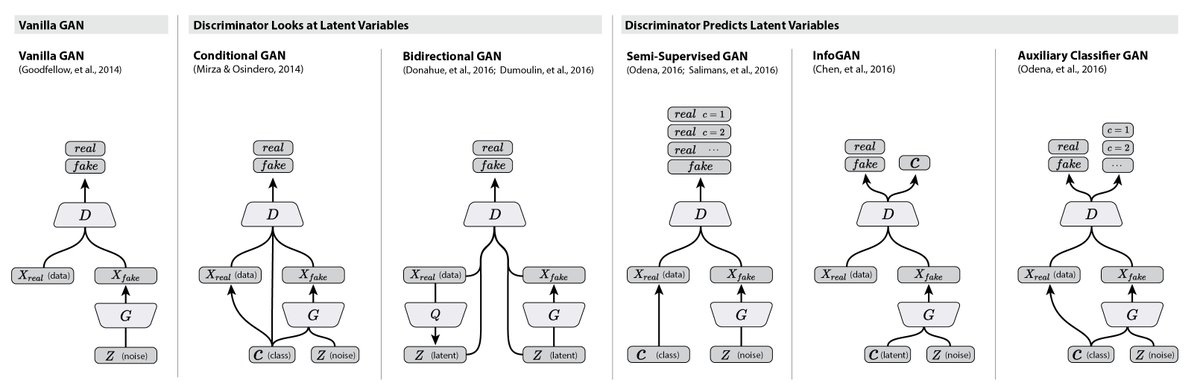
各种gan的结构：