Alignment in LLM

Posted on Edited on In

对齐什么？

  • 人类的沟通习惯
    • 不答非所问；不说太多废话；没有逻辑错误
    • GPT-3 -> InstructGPT
  • 人类的价值观
    • 不产生错误的、不安全的、有偏见的回答
  • 其他人类的期望💡
    • 比如：
      • 更擅长精准地使用工具（API）
      • 更擅长理解用户观看兴趣
      • 更擅长挖掘视频卖点
      • 更擅长将一个用户query转写成便于系统理解query

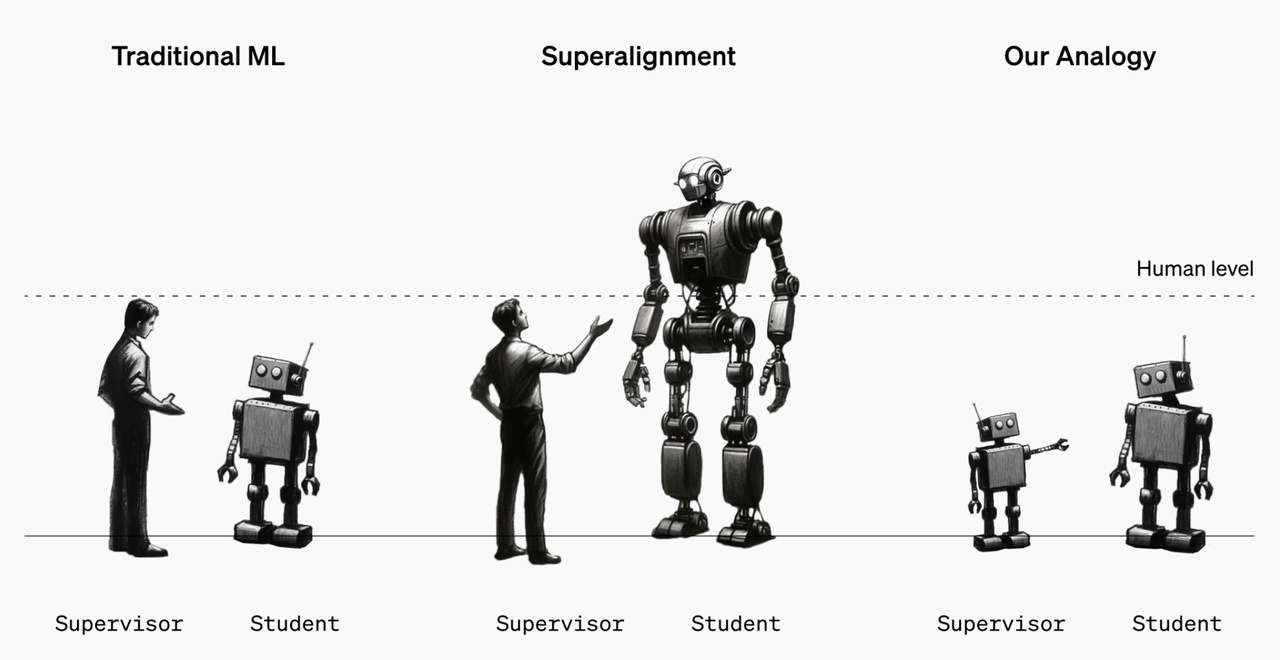
openai_alignment

对齐的成本？

InstructGPT 提到了Alignment Tax，LLM在对齐后，会在传统的NLP任务上掉点。

怎么对齐？

SFT

收集我们认为对齐了的语料，对语言模型进行SFT。
最简单的方式，但效率相对比较低，特别是对于一些抽象的任务，如简洁性、安全性。

RLHF (Preference Optimization)

来自InstructGPT的典型架构：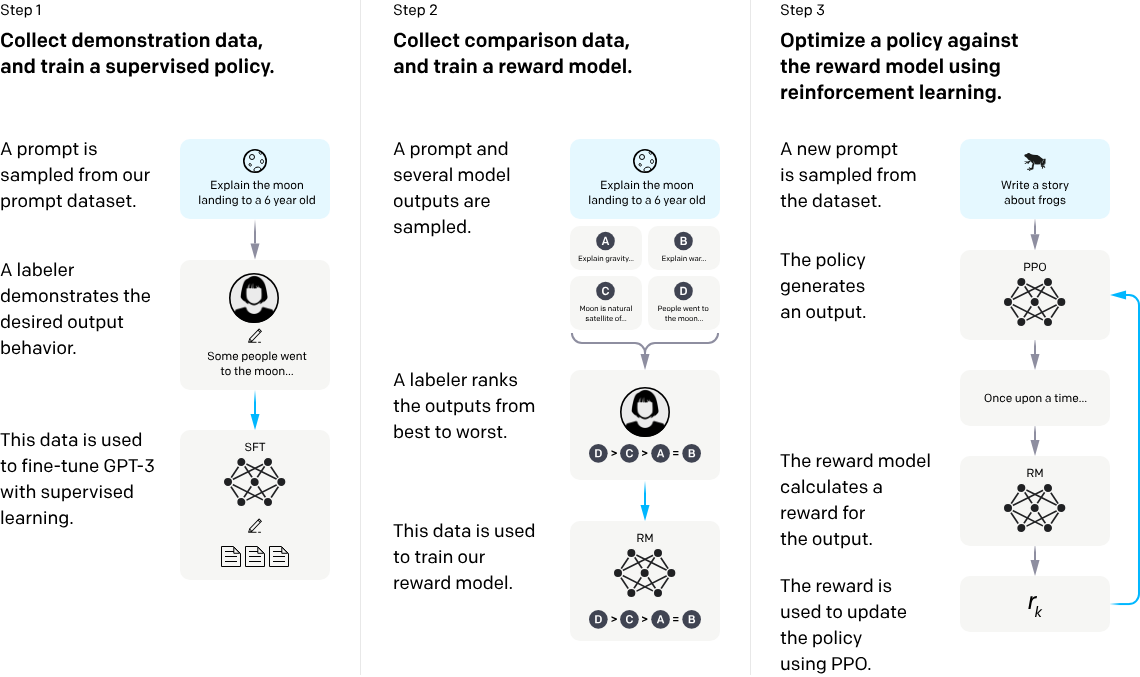
instruct_gpt

Why RLHF？

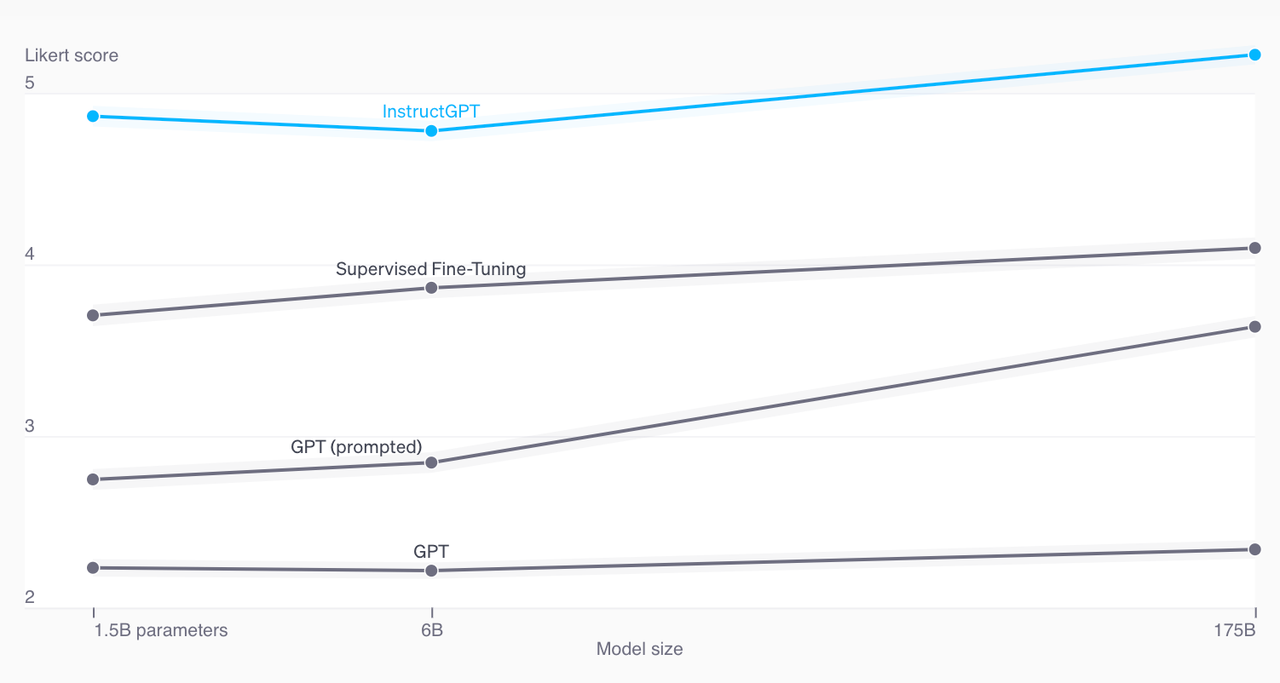
rlhf_performance

纵轴是人类偏好的得分。RLHF相比于SFT还有较大的提升空间。

Algorithms

PPO (Proximal Policy Optimization)

如果想全面理解PPO，需要的背景知识：

  • 强化学习基础概念：
    • Agent：智能体；Environment：环境；action：动作；state：状态；reward：单步奖励
    • 多步回报return(随机变量)：$u_t = \sum_t \gamma^{t-1}r_t$；
    • 回报在某个(s,a)下的期望 -> 动作价值函数：$Q_{\pi}(s,a)$
    • 动作价值函数关于动作的期望 -> 状态价值函数：$V_{\pi}(s)$
  • Policy Gradient：强化学习的一类主要分支，直接学习一个策略网络$\pi_(a|s;\theta)$使目标$J(\theta)=E_s[V(s;\theta)]=E_s[\sum_a\pi(a|s;\theta)\cdot Q_{\pi}(s,a)]$，也就是策略价值函数的期望最大。
  • Actor-Critic：Policy Gradient的一种实现架构：在如何建模建模$Q_{\pi}(s,a)$的问题上使用一个神经网络来拟合，即Critic。（如果用Monte Carlo的方式来近似$Q_{\pi}(s,a)$就是REINFORCE算法）
  • TRPO：在基础Policy Gradient的形式定义上，增加限制$\pi_(a|s;\theta)$和$\pi_(a|s;\theta_{old})$差异的约束（KL散度），使得梯度更新稳定，不会有很大毛病。
    ppo
  • PPO：将TRPO里的硬约束软化，整体算法更简洁。PPO是OpenAI内部常用的强化学习算法，用于LLM属于拿来主义。
  • Reward Model：通常和agent最终要达成的目标高度正相关。LLM为了适配RL框架，需要用偏好数据训练一个奖励模型。
  • Bradley-Terry model：最常用的LLM奖励模型建模方式，对一条偏好数据：$(x,y_w, y_l)$，奖励模型的损失函数为：$-log(\sigma(r(x,y_w)-r(x,y_l))$。注意这里的奖励函数差的形式，下文有用。

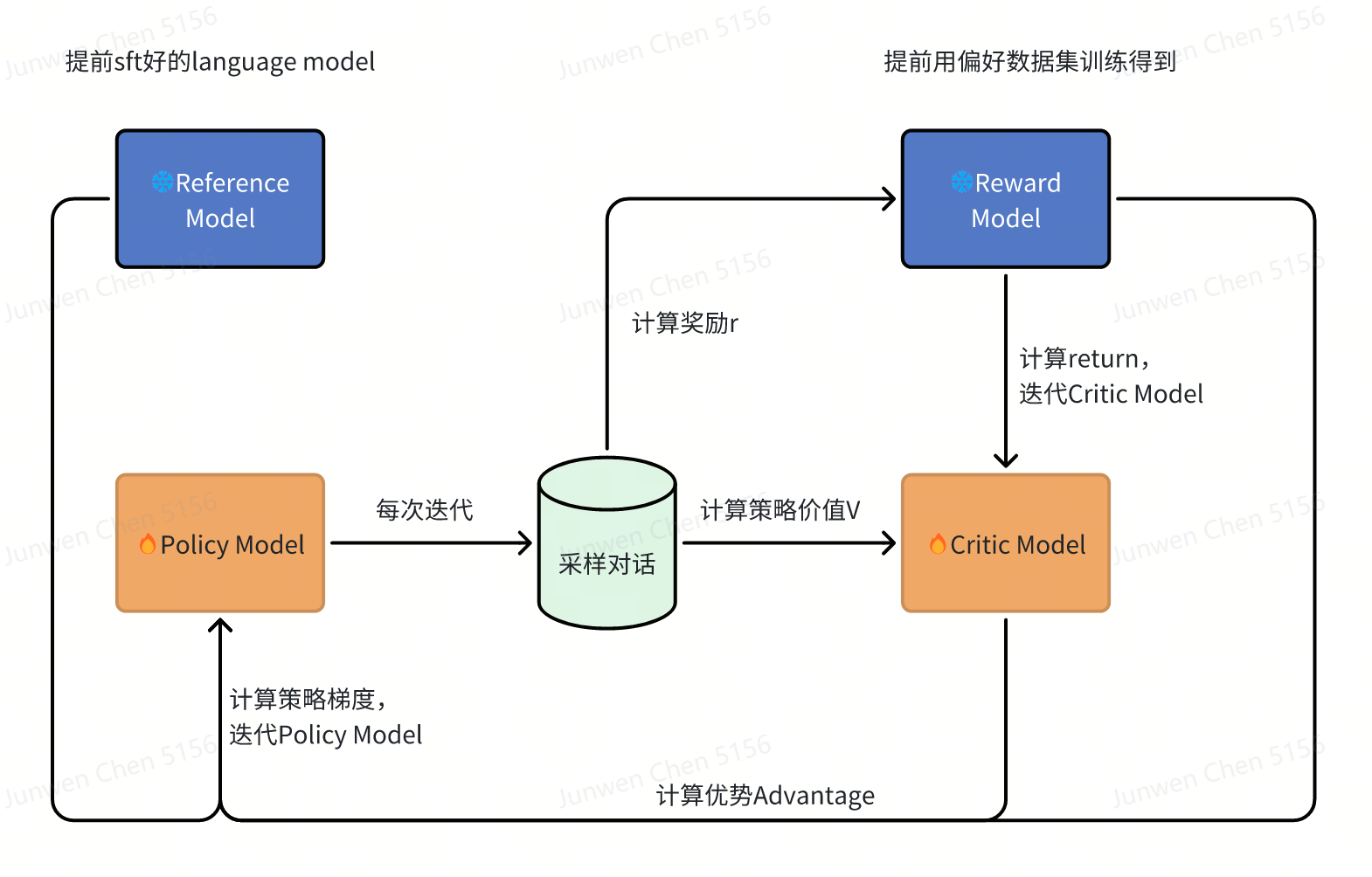
ppo_arch

PPO各个模块：

  • Reward Model是提前训练好的：$L(\psi)=log;\sigma(r(x,y_w)-r(x,y_l))$
    • 实际训练的时候还会再加一个语言模型的损失函数
    • 最终的奖励需要再考虑一个KL散度的惩罚：$r_{total} = r(x,y) - \eta KL(\pi_{\phi}^{RL}(y|x),\pi_{\phi}^{SFT}(y|x))$
  • Reference Model就是某个已经SFT好的语言模型。
  • Policy模型的训练：
    • 以KL惩罚项的形式为例（还有clip形式）：
      • $L_{ppo-penalty}(\theta) = \hat E_t [\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\hat A_t] - \beta KL(\pi_{\theta_{old}}(\cdot|s_t), \pi_{\theta}(\cdot|s_t))$
        • 其中，$\hat A_t$是优势函数的近似，这里用GAE（Generalized Advantage Estimation）：$\hat A_t^{GAE(\gamma, \lambda)} = \sum_{l=0}^{\infty}(\gamma\lambda)^l\delta_{t+l}$
        • $\lambda$是指数滑动平均的超参，$\gamma$是折扣系数
        • $\delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)$就是TD error
  • Critic模型的训练：$L_{critic(\phi)} = \hat{E_t}[||V_{\phi}(s_t)-\hat R_t||^2]$
    • $\hat R_t$是状态$s_t$下的实际多步回报（return）： $\hat R_t = \sum_{l=0}^{\infty}\gamma^l r_{t+l}$

总结下PPO的特点：

  • 具备了TRPO稳定更新的优势，相比之下更简洁了，但对于LLM来说还是很复杂。
  • 做一次训练，用到了4个模型，中间某个模型没训好就会导致最终效果不好，训练的难度比较大。
  • 每次训练迭代，需要先采样模型输出，整体训练速度会相对慢。

有哪些知名模型采用了？

  • Instruct-GPT / GPT-3.5
  • LLAMA3
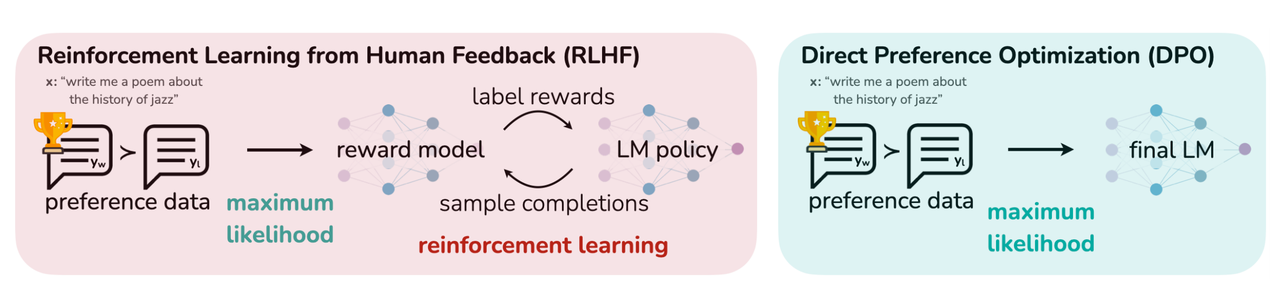
DPO (Direct Preference Optimization)

相比PPO干掉了Reward Model。

dpo

省去推导过程：$r(x,y) = \beta log\frac{\pi_r(y|x)}{\pi_{ref}(y|x)}+\beta log Z(x)$，其中$Z(x) = \sum_y \pi_{ref}(y|x) exp(\frac{1}{\beta}r(x,y))$，是配分函数，跟具体的y取值无关。用一个减法形式可以消掉配分函数：$r(x,y_w) - r(x,y_l) = \beta log\frac{\pi_r(y_w|x)}{\pi_{ref}(y_w|x)} - \beta log\frac{\pi_r(y_l|x)}{\pi_{ref}(y_l|x)}$，也就是说两个回答的奖励函数的差，和这两个回答在当前模型上的似然与参考模型的似然的差的差，正相关。这里既要求当前模型在好的回答上比坏的回答似然更高，也要求当前模型比老模型的似然更高。

带入Bradley-Terry model的损失函数，得到DPO的损失函数，对一条偏好数据：$(x,y_w, y_l)$，$L_{DPO}(\pi_{\theta},\pi_{ref}) = -log(\sigma(\beta log\frac{\pi_{\theta}(y_w|x)}{\pi_{ref}(y_w|x)} - \beta log\frac{\pi_{\theta}(y_l|x)}{\pi_{ref}(y_l|x)}))$

这里的所谓重参数的地方是：原来是先训练好一个$r_(\phi)$函数，然后用$r_(\phi)$的ground truth $r^*$来优化$\pi_(\theta)$。现在重新把目标用$r_(\phi)$来表示，$r_(\phi)$又可以消掉，目标最终$\pi_(\theta)$表示，整个过程中就可以省去奖励模型，直接学习参数$\theta$。

DPO损失函数的梯度拆解：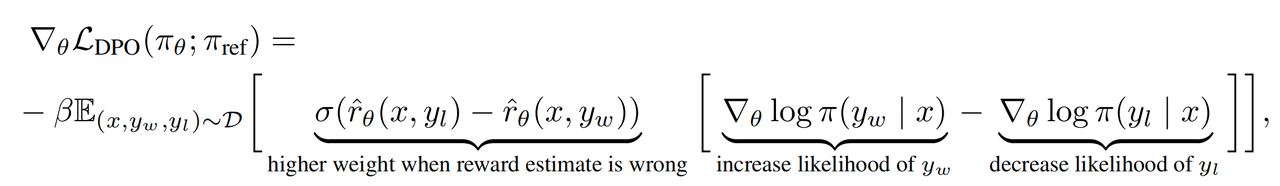
dpo_loss

其中$\hat r_{\theta}(x,y) = \beta log\frac{\pi_{\theta}(y|x)}{\pi_{ref}(y|x)}$

也就是说DPO，会增加$y_w$的似然，减少$y_l$的似然，且奖励预估偏差越大，整体权重也会越大。

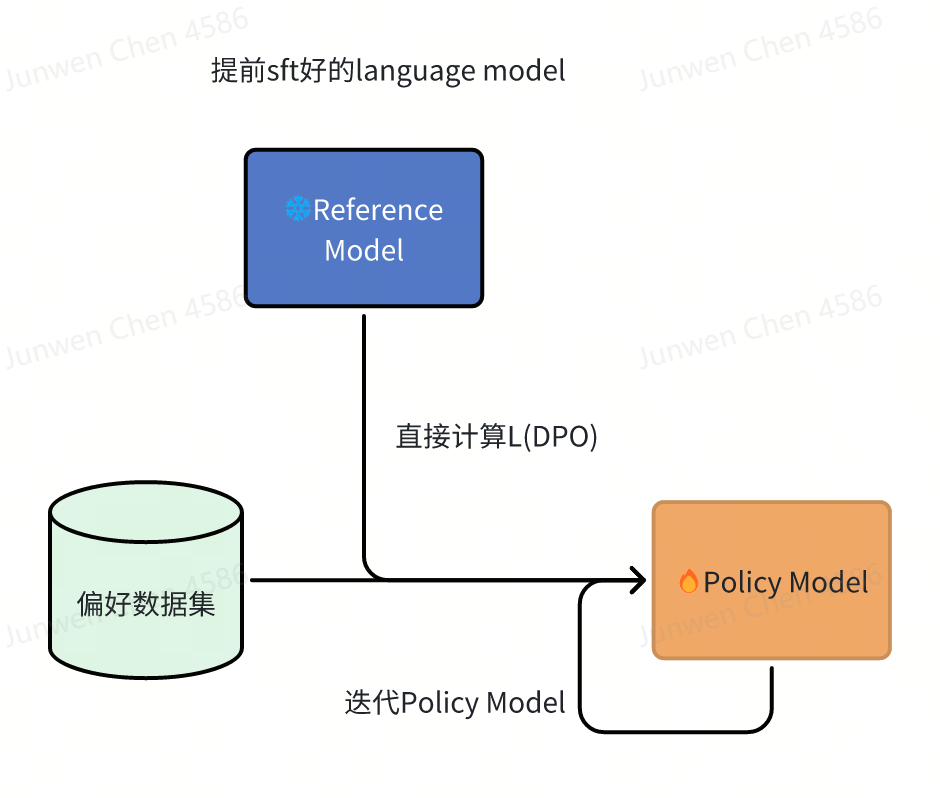
dpo_arch

这里还有个细节：偏好数据集理论上都应该是Reference Model采样出来的。所以实践中，要么自己采样一些不同的输出，去标注；如果要用现成的偏好数据集（学术圈很常用），需要把要用的Reference Model在偏好数据集上sft下。

总结下DPO的特点：

  • 去掉了reward model，整体架构更简洁了。
  • 实战中发现比PPO更容易过拟合。
  • 还存在SimPO提出的奖励函数和inference时目标不完全对齐的问题。

有哪些知名模型采用了？

  • LLAMA3
SimPO

相比于DPO，又更近一步干掉了Reference Model。

直接用平均似然作为奖励函数。

$$r_{SimPO}(x,y) = \frac{\beta}{|y|} \sum_{i=1}^y log{\pi_{\theta}(y_i|x,y_{<i})}$$
SimPO的损失函数：对一条偏好数据：$(x,y_w, y_l)$，
$$L_{SimPO}(\pi_{\theta}) = -log(\sigma(\frac{\beta}{|y_w|} \sum_{i=1}^{y_w} log{\pi_{\theta}(y_i|x,y_{<i})} - \frac{\beta}{|y_l|} \sum_{i=1}^{y_l} log{\pi_{\theta}(y_i|x,y_{<i})} - \gamma))$$

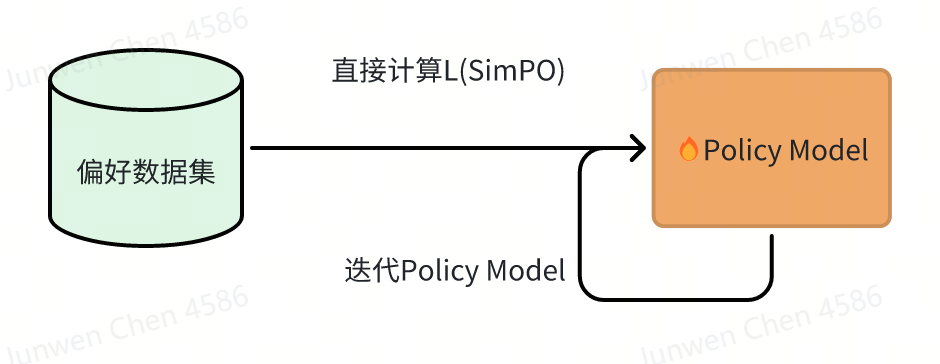
simpo_arch

SimPO相比DPO的优势：

  • 少了Reference Model，整体架构更简洁了
  • reward相对于DPO和最终infer时的目标更一致。DPO在一些情况下，reward大但似然小。

常见的Preference Optimization的目标函数：

alignment_target_function

关于应用的思考

  • 在llm生成推荐的场景中，我们可以通过生产结果的实际后验统计效果，来构建一个推荐偏好数据集，对llm进行训练。比如点赞多的推荐为正例，点踩多的为负例。这样可以免除人工标注。
  • 现在的偏好，似乎还是在学人类整体（群体）的偏好。有没有可能探索一下个人的偏好？比如每个人的偏好就用一个uid的token表示，我们在训练中，将llm 参数fix，只tune这个token的embedding？

Reference