PPO in LLM详解

Posted on Edited on In

策略梯度的通用形式

$\nabla_\theta J(\theta)=E_{\tau \sim \pi_\theta}[\sum_{t=0}^T\nabla_\theta log \pi_\theta(a_t|s_t)\Phi_t]$

  • 其中，$\Phi_t$可以是各种形式：
    • 如 $\Phi_t = R(\tau)$
    • 或者 $\Phi_t = \sum_{t’=t}^T R(s’_t, a_t’)$
    • 或者 $\Phi_t = \sum_{t’=t}^T R(s’_t, a_t’) - b(s_t)$
    • 也可以是 $\Phi_t = A(s_t,a_t)=Q(s_t,a_t)-V(s_t)$

用优势函数可以降低 $\Phi_t$ 的方差。

策略梯度的 $\Phi_t$ 如果用蒙特卡洛的方式来估算，就是REINFORCE算法；如果用一个critic model来学，就是Actor-Critic架构。PPO本质上采用了Actor-Critic架构。

RLHF到底为LLM贡献了啥？

对齐！对齐人类的沟通方式，对齐人类的价值体系，比如安全性、真实性等等。

PPO的由来

随机梯度策略 —为了限制梯度更新过大—> TRPO —将约束直接加载目标函数里（大幅简化）—> PPO

总而言之，TRPO和PPO的核心思想都是采用更小更稳定的策略更新，只不过PPO实现更简单。

moutain

PPO算法

ppo_algo

其中：

  • Policy模型的训练：
    • CLIP形式：$L_{ppo-clip}(\theta) = \hat E_t[min(\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\hat A_t, clip(\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}, 1-\epsilon, 1+\epsilon)\hat A_t)]$
      • $\hat A_t$ 是优势函数的近似，这里用GAE（Generalized Advantage Estimation）：
        • $\hat A_t^{GAE(\gamma, \lambda)} = \sum_{l=0}^{\infty}(\gamma\lambda)^l\delta_{t+l}$
        • $\lambda$ 是指数滑动平均的超参，$\gamma$ 是折扣系数
        • $\delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)$
        • 为什么用GAE估计优势函数？
    • 惩罚项形式：$L_{ppo-penalty}(\theta) = \hat E_t [\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\hat A_t] - \beta KL(\pi_{\theta_{old}}(\cdot|s_t), \pi_{\theta}(\cdot|s_t))$
  • Critic模型的训练： $L_{critic(\phi)} = \hat{E_t}[||V_{\phi}(s_t)-\hat R_t||^2]$
    • $\hat R_t$ 是状态$s_t$下的实际收益：$\hat R_t = \sum_{l=0}^{\infty}\gamma^l r_{t+l}$
  • Reward模型是提前训练好的：$L(\psi)=log;\sigma(r(x,y_w)-r(x,y_l))$
    • 实际训练的时候还会再加一个语言模型的损失函数
    • 最终的奖励需要再考虑一个KL散度的惩罚：$r_{total} = r(x,y) - \eta KL(\pi_{\phi}^{RL}(y|x),\pi_{\phi}^{SFT}(y|x))$

PPO算法的优点：

  • 通过clip操作，避免了过大的policy更新

    • min + clip的最终效果：（横坐标是ratio，纵坐标是目标值）

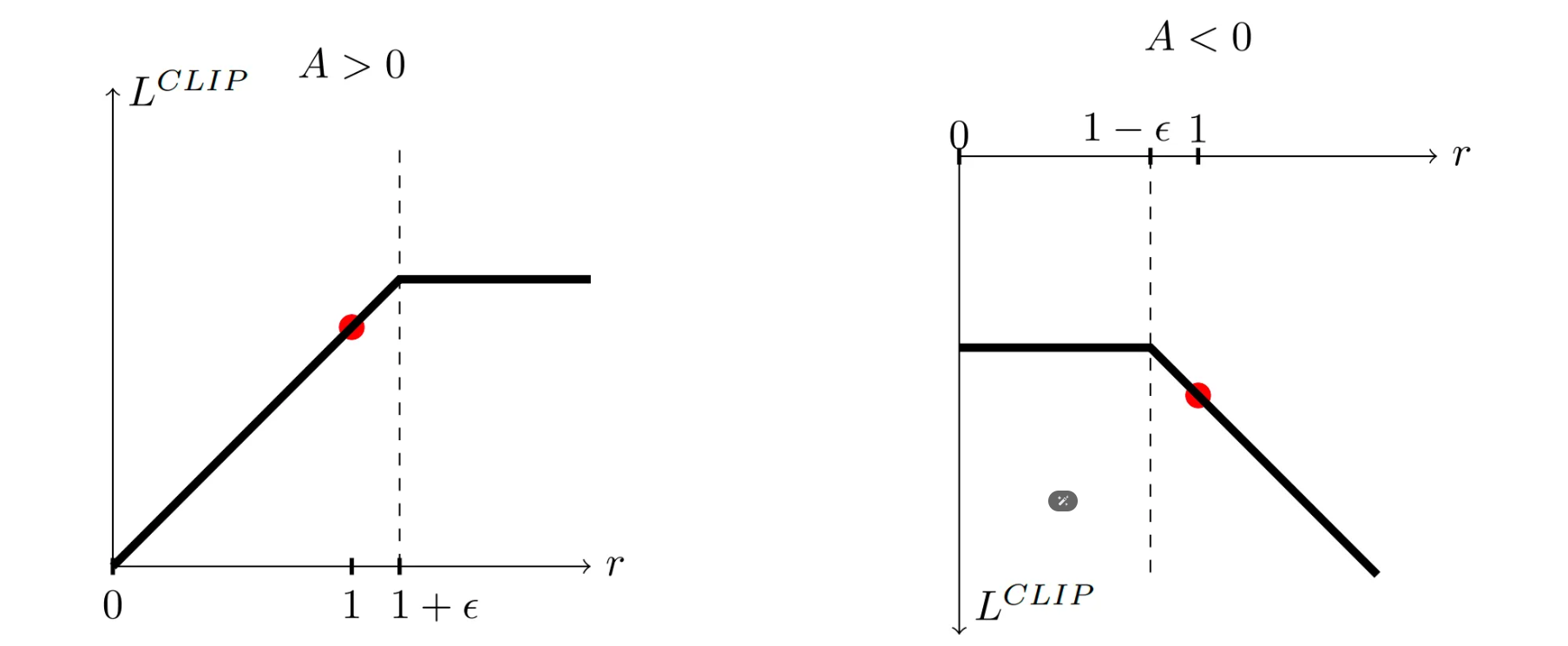
    • ppo_clip

    • 当A>0，说明当前动作表现优于平均水平。如果此时ratio较大，说明新策略相对老策略在这个动作的概率已经比较大，我们不要过于贪心，这里就将梯度设成0，不再更新。

    • 当A<0，说明当前动作表现差于平均水平。如果此时ratio较小，说明新策略相对老策略在这个动作的概率已经比较小，我们不要过于贪心，这里就将梯度设成0，不再更新。

  • 比TRPO更简洁，但具有了TRPO的优点：稳定。

PPO代码实现

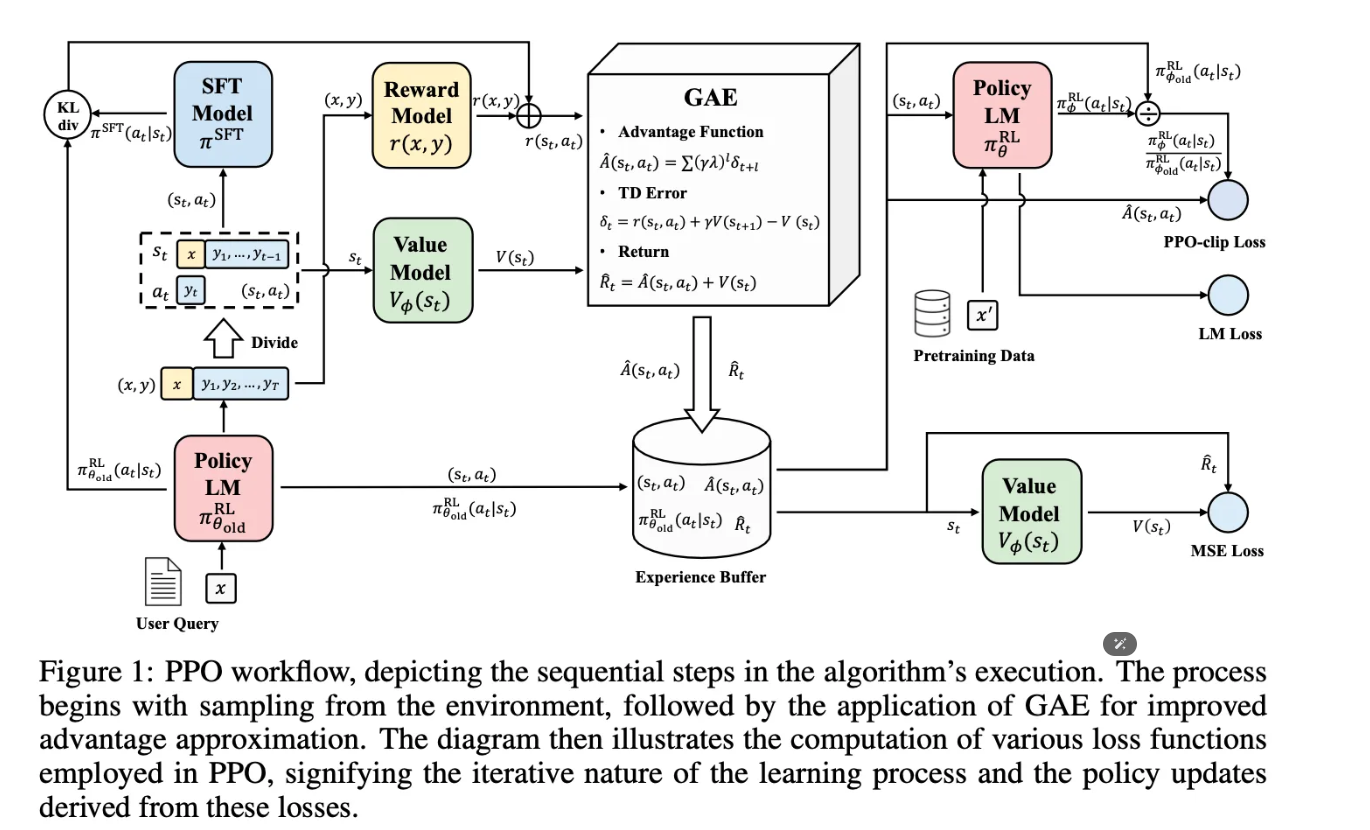
ppo_code_arch

从图上（结合代码）看，一共涉及4个模型：

  • policy model （RLHF最终获取的语言模型）
  • critic model （图中Value Model，计算value，参数可训）
  • reference model （图中SFT Model，用于计算KL，参数固定）
  • reward model （计算reward，参数固定）

Loss一共有3个：

  • PPO-clip Loss （作用于policy model）
  • LM Loss （作用于policy model，通常是可选项）
  • MSE Loss （作用于critic model）

代码流程：

  • make experiences

    • 随机采样prompt
    • 生成对应的response
    • 根据response计算reward（reward model）和value（critic model）
    • 计算policy model的probs和ref model的probs的kl散度

  • 根据experience生成新的训练数据

    • 计算advantages和returns

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      def get_advantages_and_returns(self, rewards: List[float], values: List[float]):
              '''
              Copied from TRLX: https://github.com/CarperAI/trlx/blob/main/trlx/models/modeling_ppo.py
              '''
              response_length = len(values)
              advantages_reversed = []
              lastgaelam = 0
              for t in reversed(range(response_length)):
                  nextvalues = values[t + 1] if t < response_length - 1 else 0.0
                  delta = rewards[t] + self.gamma * nextvalues - values[t]
                  lastgaelam = delta + self.gamma * self.lam * lastgaelam
                  advantages_reversed.append(lastgaelam)

              advantages = advantages_reversed[::-1]
              returns = [a + v for a, v in zip(advantages, values)]
              assert len(returns) == len(advantages) == len(values)
              return advantages, returns

  • train step

    • policy_model和critic_model执行前向计算
    • criterion
      • 计算vf_loss
        • vf_loss1 = (values - returns) ** 2
      • 计算pg_loss1
        • pg_loss1 = advantages * ratio
    • 使用优化器梯度回传

参考