大模型中的系统一和系统二

Posted on Edited on In

一个有趣&有用的topic，跟大家一起探讨~

引子

system_12_book

丹尼尔卡尼曼在《思考，快与慢》中引入了人脑的系统一和系统二的概念：

  • 系统一：不费力的反应，比如老司机开车、大人回答一位数的加减法问题等。
  • 系统二：需要动用注意力/心智资源，去仔细思考，比如回答为什么一个指标变化了，做n位的乘法题。

大语言模型上的类比：

  • 系统一：**不生成中间 Token **而直接生成答案的方案。$S_{I}(x) = p_{\theta}(x) \rightarrow y$
  • 系统二：生成中间 Token 的方案，包括执行搜索或多次提示来生成最终响应。$S_{II}(x;p_{\theta}) \rightarrow z,y$

人脑的系统一和系统二有一个特质是：系统二在足够熟练后有可能向系统一转变，在心理学上称为 “Automaticity”（自动化）。比如新手司机逐渐熟练开车后，开车也不再那么费精力。这个过程可以形象地理解成是神经回路的固化：当我们不熟练时，某个process可能是需要在多种选项中进行搜索的，我们对不同选项的优劣还没那么清楚；当我们足够熟练以后，某个process的所有选项的优劣我们已经了然于胸，因此不用怎么搜索，能够很快地得到结果。

总结下：所谓系统二的做法其实就是要多输出很多中间输出，或者增加对话的轮数，进行自问自答。这些增加的输出可以理解成是模型的思考流。而系统一则是跳过所有中间输出，直接得到结果。

LLM在系统二上的探索

思维链（Chain of Thought，CoT）

Chain-of-Thought Prompting Elicits Reasoning in Large Language Models
Large Language Models are Zero-Shot Reasoners

  • Few-Shot:
    • 提供对问题进行拆解的解答样例。
  • Zero-Shot:
      • Please think step by step; + Give me the detailed reasons.

cot_examples

思维树（Tree of Thought，ToT）

Tree of Thoughts: Deliberate Problem Solving with Large Language Models
https://github.com/princeton-nlp/tree-of-thought-llm

tot

  • 定义：state表示当前的部分解法。$s=[x,z_{1…i}]$
  • 流程：
    • 问题拆解：分析下task的特质，定义好thought是啥。thought的大小应该是足够小到让llm可以生成diverse的候选；但同时足够大到让llm可以评估是不是向着问题解决更近了一步。
    • 生成thought候选：
      • sample：每个step独立同分布采样k个though候选，$z^{(j)} \sim p_{\theta}^{CoT}(z_{i+1}|s)$。适用于思考空间比较大的情况，比如创造性写作，每个thought是一个段落。
      • propose：用一个所谓的“propose prompt”同时生成一系列的thoughts，$[z^{(1)},z^{(2)},…,z^{(k)}] \sim p_{\theta}^{propose}(z_{i+1}^{(1…k)}|s)$。适用于思考空间比较小的情况，用于避免重复的thought候选。比如玩24点，可能的解法是比较有限的。
    • 状态评估：
      • 给每个状态独立地Value (pointwise)：
        • $V(p_{\theta},S)(s) \sim p_{\theta}^{value}(x|s) \forall s \in S$
        • 比如从1-10打分，或者sure/likely/impossible分类
      • 结合所有的候选状态进行Vote (listwise)：
        • $V(p_{\theta},S)(s) = 1[s=s^*]$
    • 搜索算法：
      • BFS：
        • 每个step维护一个最promising的状态的set。
      • DFS
        • 先探索最promising的state

tot_dfs_bfs

  • 效果：
    • 在一些需要强推理的任务上效果显著，比如计算24点，问题解决率从CoT的4%上涨到74%。

24点：

tot_24

创意写作：
tot_creative_writing

思维图（Graph of Thought，GoT）

Graph of thoughts: Solving elaborate problems with large language models.
https://github.com/spcl/graph-of-thoughts

  • 思考结构可以是任何的图。支持了refining和merging

got

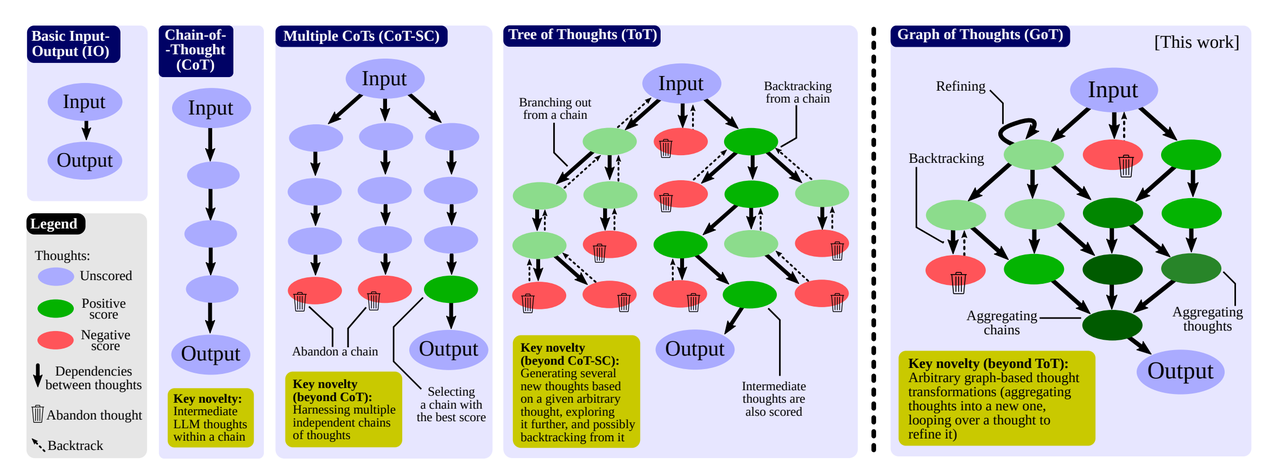
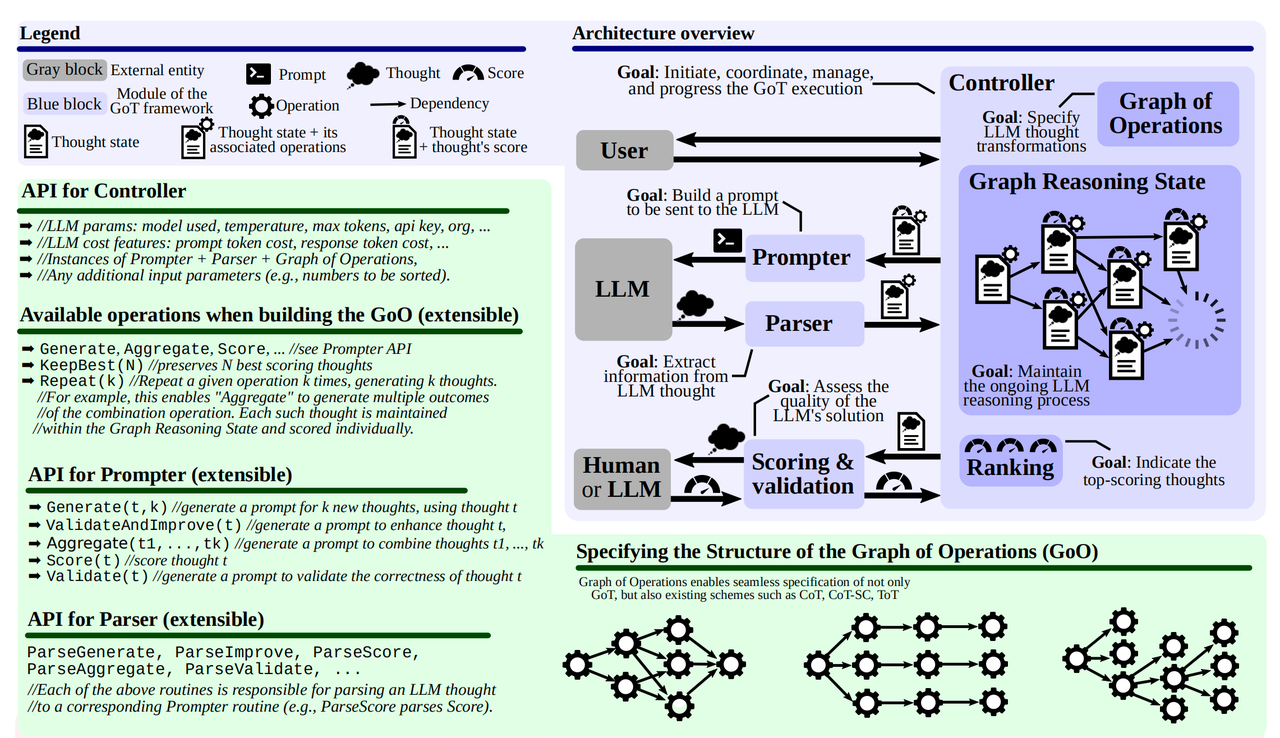
  • 搞了一个框架，定义了一些列接口用于构建图：
    • Generate，1 -> k
    • Validate, 当前节点自我检查
    • Aggregate, k -> 1
    • Score, 评估当前节点

got

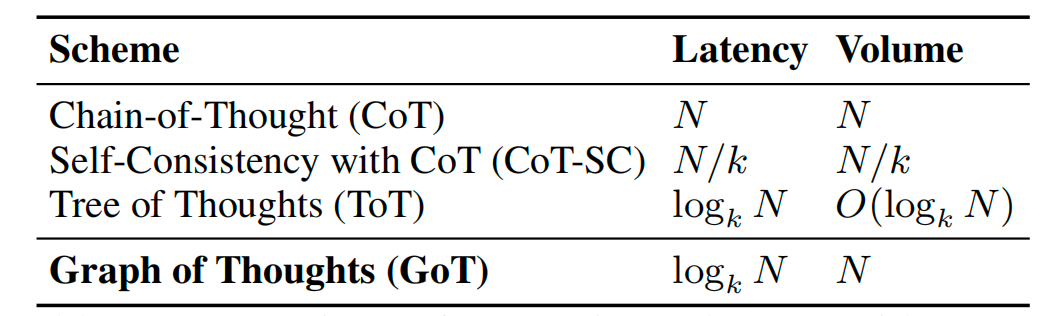
  • Latency-Volume Tradeoff
    • N（节点个数，thought个数）
    • volume的定义是在途中有多少个节点有路径可以到达一个指定的节点。

got

数组排序的例子：

got

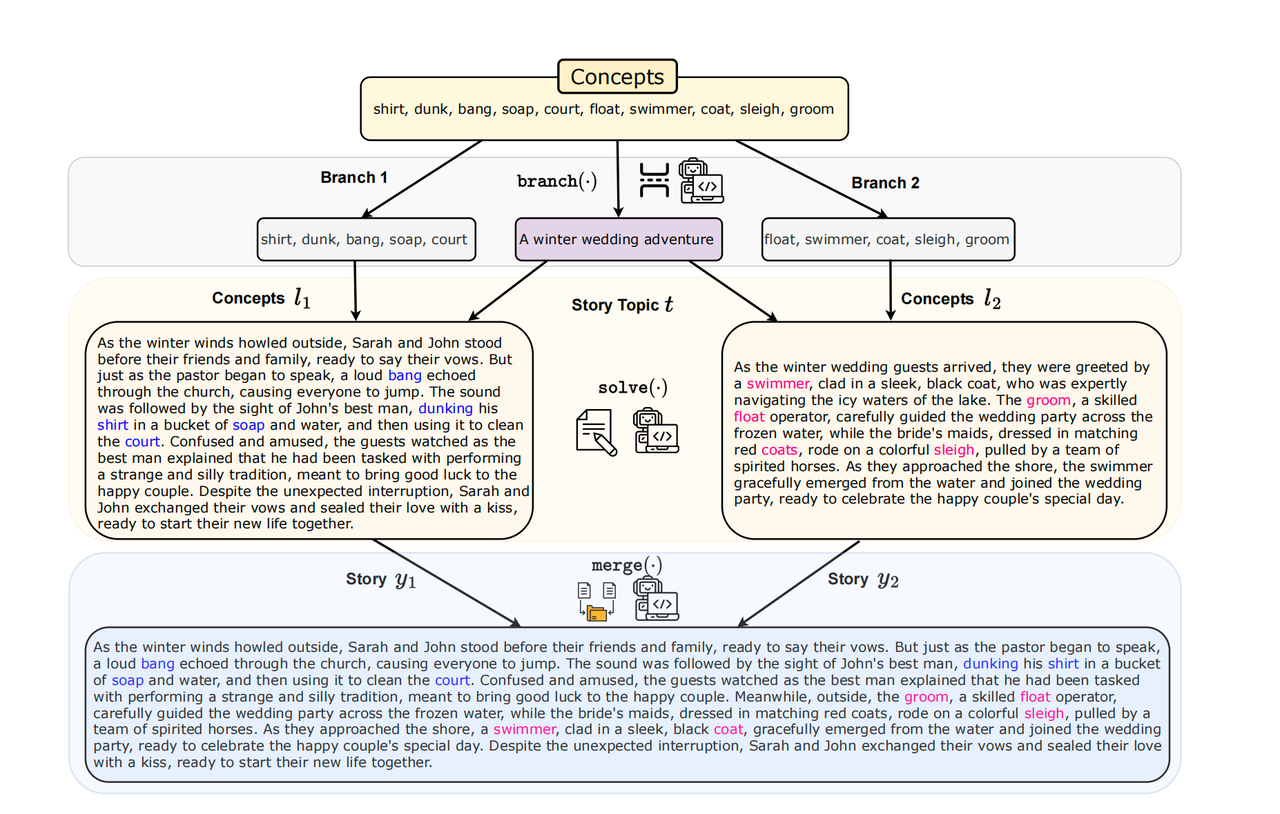
Branch-Solve-Merge

Branch-Solve-Merge Improves Large Language Model Evaluation and Generation

  • Branch模块：给定任务，生成一些子任务，每个子任务是一个branch，每个branch输入原始问题，生成新的prompt；
  • Solve模块：针对每个branch模块生成的prompt，生成答案；
  • Merge模块：对所有Solve模块生成的prompt进行合并，给出最终的答案。

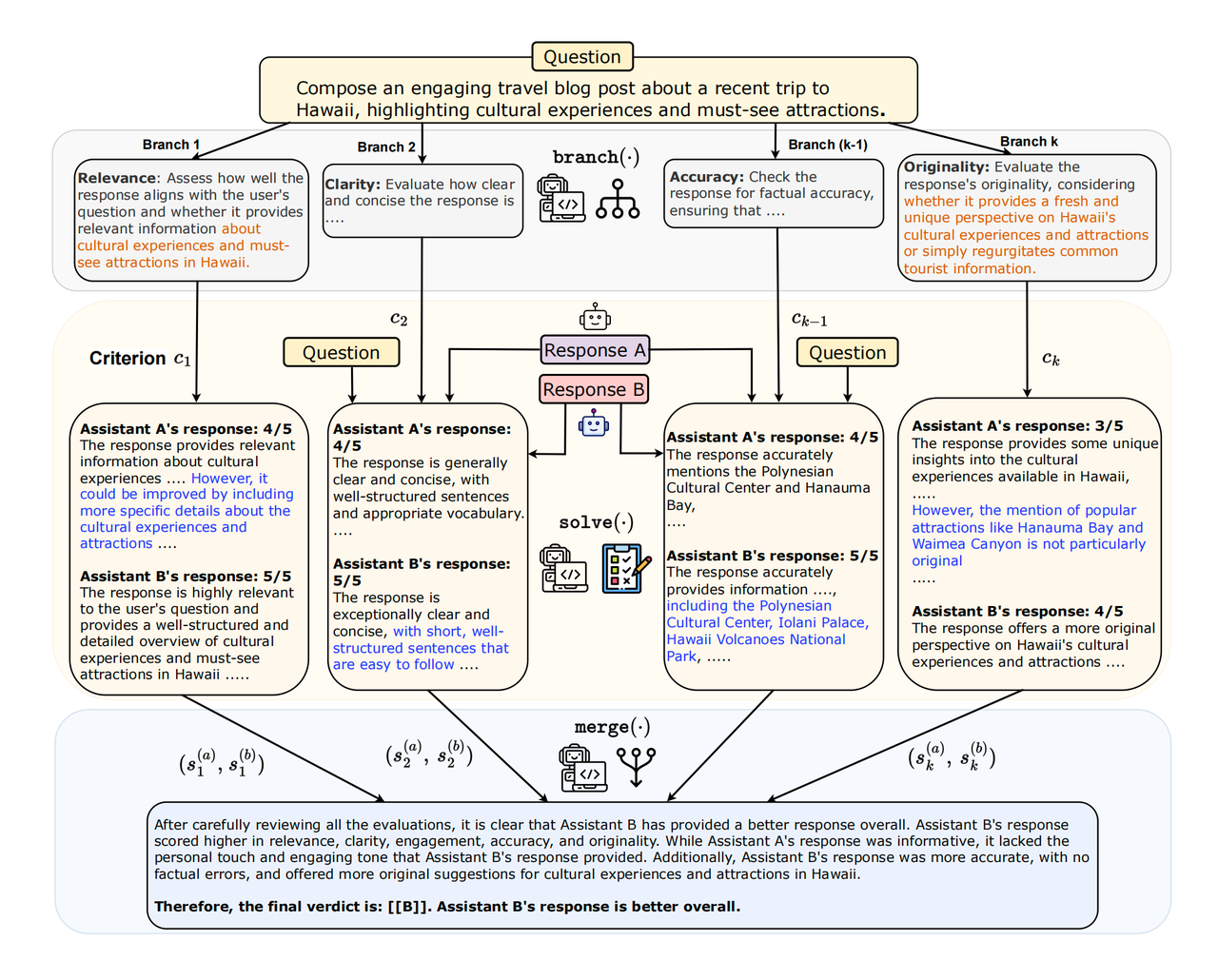
branch_solve_merge

创意写作的例子：

branch_solve_merge

System 2 Attention

System 2 Attention (is something you might need too)

  1. 先重新生成输入x’，将无关内容去除（所谓的attention）
  2. 重新让大语言模型生成结果：$y \sim LLM(x’)$

system_2_attention

Rephrase and Respond

Rephrase and respond: Let large language models ask better questions for themselves.

  1. 重写问题
  2. 给出回答

和CoT互补，可以一起用。
rephrase_respond

系统二的有效性看起来是比较solid的。那么大模型是否也能做Automaticity的类比，将系统二的能力，迁移到一个更低成本的系统一呢？

From System 2 to System 1

方案一

Distilling System 2 into System 1

做法：

  • 收集一些无监督数据X，用系统二生成回复：$y^i_{S_{II}}=S_{II}(x^i;p_{\theta}), \forall x_i \in X $
  • self-consistency约束：对一个输入，采样N次，然后使用出现次数最多的那个答案。
  • 系统一和系统二是同一个模型！
  • 用生成的$(X_{II},Y_{II})$来finetune LLM，得到系统一。

效果：

  • COT蒸馏的效果基本上还是原来系统一的水平。
  • Branch-Solve-Merge的效果接近甚至超过原来系统二的水平。
  • System 2 Attention 蒸馏效果超过系统二
  • Rephrase and Respond 蒸馏效果接近甚至超过系统二

方案一相当于是我自己先按照详细的思路先计算一堆题目，然后去背这些题目的答案，背多了也学会套路了。但这些系统二的思路，系统一其实并不清楚。（所以其实还有种finetune的办法是把解法也加到输入里）

这里的局限性以乘法题为例，我可能能背出99乘法表，也知道多位乘法的算法，但给我一个多位乘法的题目，我总是需要拿个草稿纸把中间过程算一下，无法直接给出答案。

方案二

Chain of Preference Optimization: Improving Chain-of-Thought Reasoning in LLMs
https://github.com/sail-sg/CPO

做法：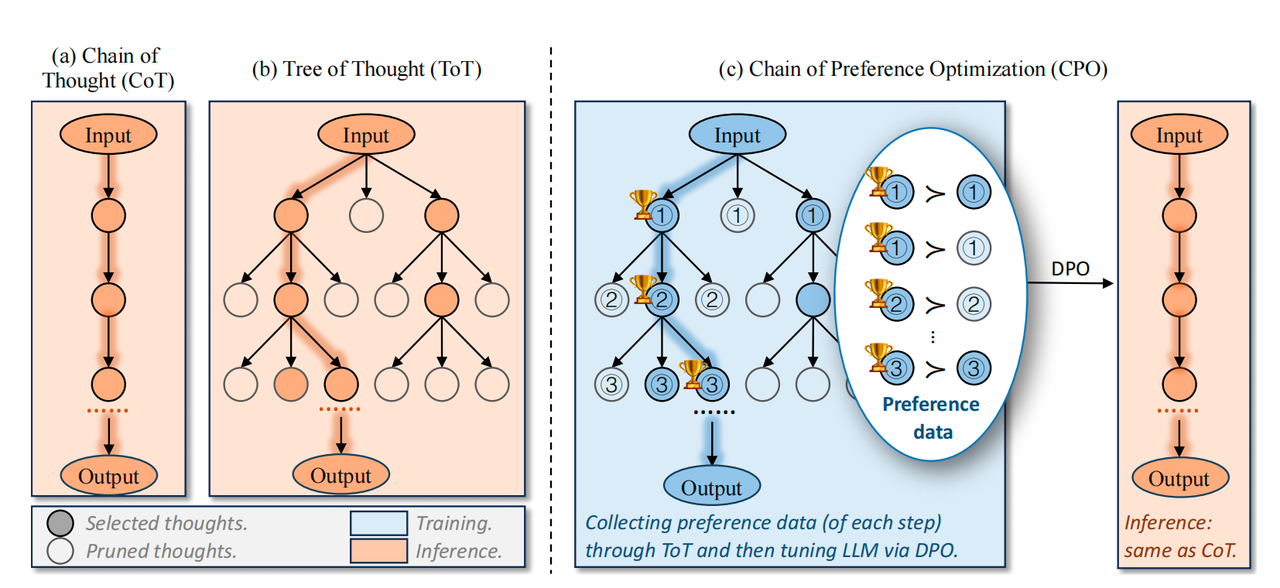
cpo

    1. 生成Thoughts：
    2. $z^{j}i \sim \pi{\theta}(z_i|s_{i-1}) = \pi_{\theta}(z_i|x,z_1,…,z_{i-1}), ; for ; j=1,…,k$
    1. state评估：
    • 独立打分
    1. 搜索，然后收集数据：
    • 用BFS搜索，收集在状态$s_{i-1}^w$下的偏好数据对$(z_i^w, z_i^l)$
    1. 用CPO目标进行训练（其实就是DPO）：
    • $L_i(\pi_{\theta};\pi_{ref}) = -log \sigma(\beta log\frac{\pi_{\theta}(z_i^w|x,s^w_{i-1})}{\pi_{ref}(z_i^w|x,s^w_{i-1})} - \beta log\frac{\pi_{\theta}(z_i^l|x,s^w_{i-1})}{\pi_{ref}(z_i^l|x,s^w_{i-1})})$
    • $L_{CPO}(\pi_{theta};\pi_{ref}) = E_{(x,z^w_i,z^l_i,s_{i-1}^w)\sim D}[L_i(\pi_{\theta};\pi_{ref})]$

效果：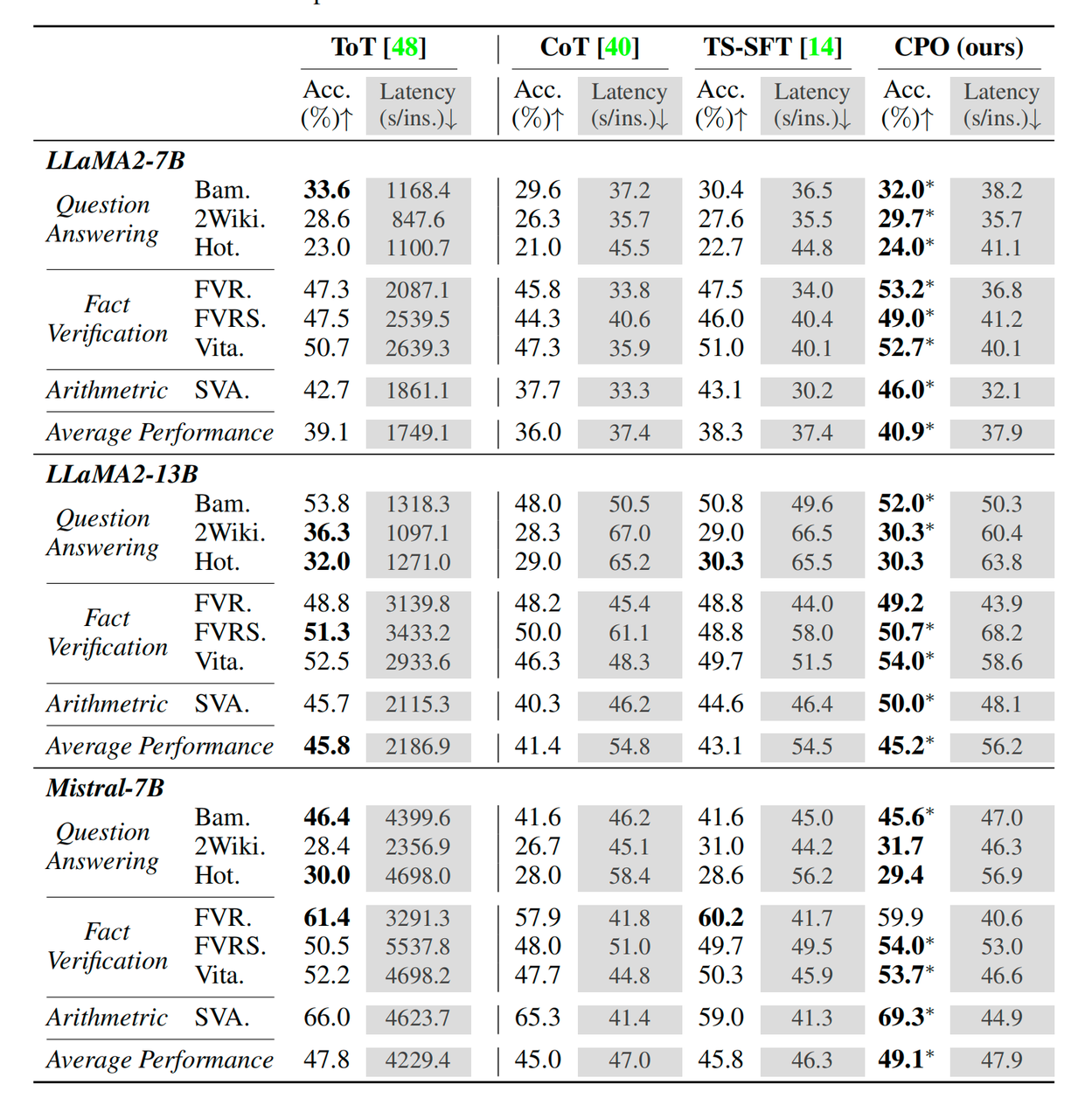
cpo_result

可见CPO在latency下降显著的情况下，还能保持较高的Acc。不过ToT的latency的确高的有点离谱。

这个思路和人脑实际发生的自动化更相似。

应用思考

应用一

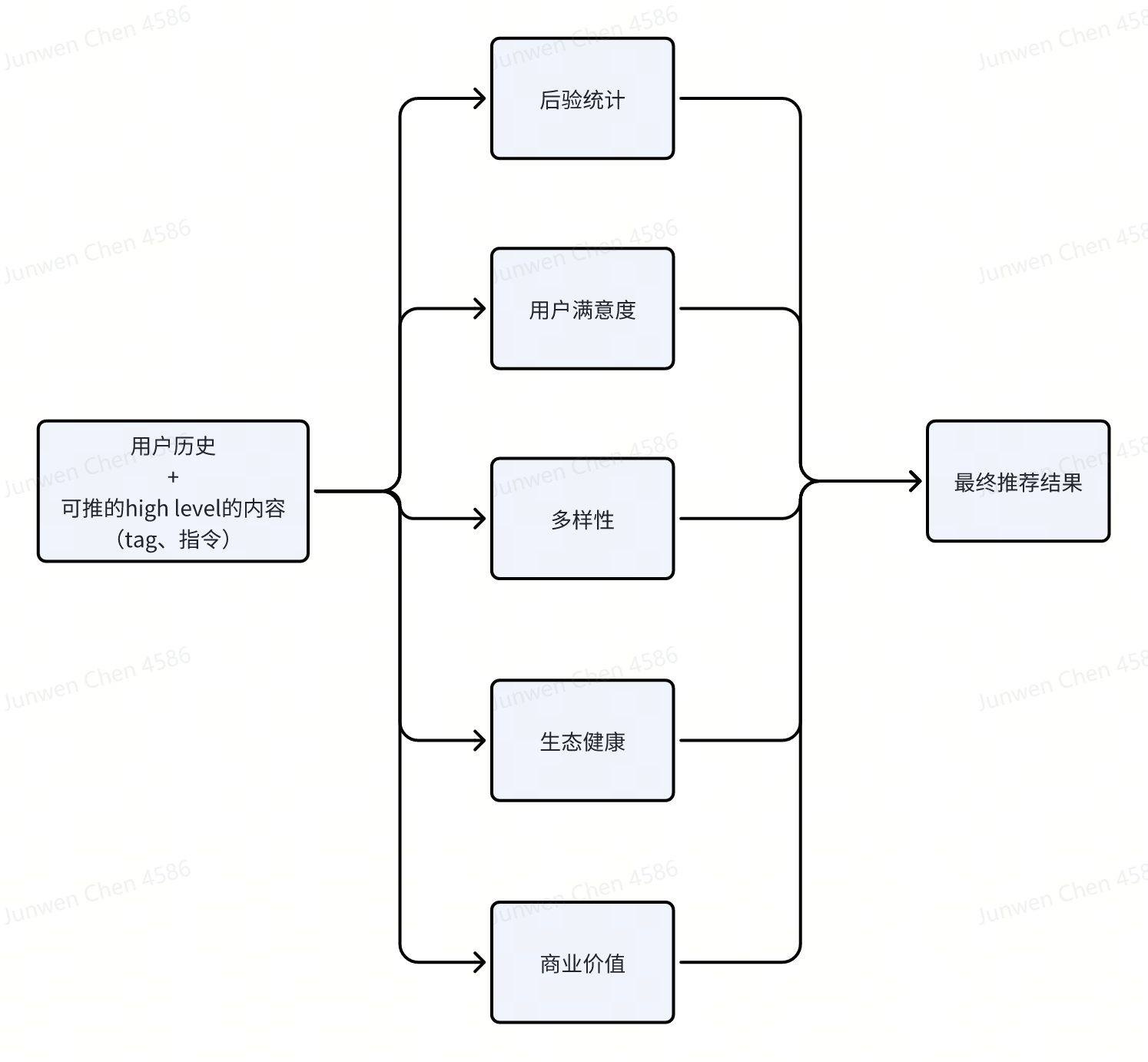
任何复杂的推理任务，比如说我们想用大语言模型做推荐，也是一个复杂的逻辑推理过程。我们可以用Branch-Solve-Merge来生成多个推荐维度（用户喜欢类似的视频、多样性、informativeness），再merge成最终的推荐结果：

branch_solve_merge

Reference

  • Distilling System 2 into System 1
  • Chain of Preference Optimization: Improving Chain-of-Thought Reasoning in LLMs
  • Branch-Solve-Merge Improves Large Language Model Evaluation and Generation
  • System 2 Attention (is something you might need too)
  • Rephrase and respond: Let large language models ask better questions for themselves.
  • Chain-of-Thought Prompting Elicits Reasoning in Large Language Models
  • Tree of Thoughts: Deliberate Problem Solving with Large Language Models
  • Graph of thoughts: Solving elaborate problems with large language models.
  • Towards Goal-oriented Prompt Engineering for Large Language Models: A Survey