条件随机场 CRF总结和实现

概率无向图模型

回顾一下之前讲解的概率无向图模型：https://applenob.github.io/machine_learning/graph.html

总结一下：

最大团：无向图$G$中任何两个结点都有边连接的结点子集称为团（clique）。若团$C$不能在加入任何一个结点使其称为一个更大的团，则称$C$为图$G$的一个最大团。
概率无向图模型的联合概率分布可以表示成其最大团上的随机变量的函数的乘积形式。这也被称为概率无向图模型的因子分解。
$P(Y) = \frac{1}{Z}\prod_C\psi_C(Y_C)$，其中，$Z$是规范化因子，$Z = \sum_Y\prod_C\psi_C(Y_C)$，$\psi_C(Y_C)$称为势函数，要求势函数是严格正的（因为涉及到累乘）。

条件随机场

条件随机场（Conditional Random Field， CRF）也是一种无向图模型。它是在给定随机变量$X$的条件下，随机变量$Y$的马尔科夫随机场。

我们常用的是线性链条件随机场，多用于序列标注等问题。形式化定义：设$X=(X_1, X_2, …, X_n)$，$Y=(Y_1, Y_2, …,Y_n)$均为线性链表示的随机变量序列，若给在定随机变量序列$X$的条件下，随机变量序列$Y$的条件概率分布$P(Y|X)$构成条件随机场，即满足马尔科夫性：

$$P(Y_i|X, Y_1,…,Y_{i-1}, Y_{i+1}, …, Y_n) = P(Y_i|X, Y_{i-1}, Y_{i+1})\;\;i=1,2, …, n$$

这个式子是核心，充分理解这个式子和下面的图片

称$P(Y|X)$是线性链条件随机场。

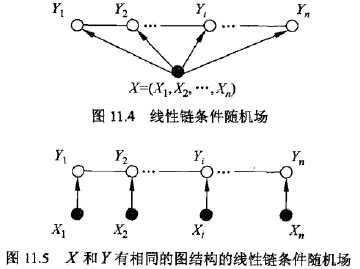
参数化形式

$$P(y|x) = \frac{1}{Z(x)}exp(\sum_{i,k}\lambda_kt_k(y_{i-1}, y_i, x, i)+\sum_{i,l}\mu_ls_l(y_i, x, i))$$

其中，$Z(x) = \sum_y exp(\sum_{i,k}\lambda_kt_k(y_{i-1}, y_i, x, i)+\sum_{i,l}\mu_ls_l(y_i, x, i))$，$t_k$是转移(transform)特征函数，依赖于当前和前一个位置，$s_l$是状态(state)特征函数，依赖于当前位置，$\lambda_k$和$\mu_l$是对应的权值。

从模型的参数化形式可以看出，线性链条件随机场也是对数线性模型。

简化形式

所谓简化形式即，将局部特征特征统一成一个全局特征函数。
设有$K_1$个转移特征，有$K_2$个状态特征，$K=K_1+K_2$。

$$f_k(y_{i-1}, y_i, x, i) = \left\{\begin{matrix}t_k(y_{i-1}, y_i, x, i),\;\;k=1,2,…,K_1\\ s_l(y_i, x, i),\;\; k=K_1+l,\; l=1,2,..,K_2 \end{matrix}\right.$$

对所有在位置$i$的特征求和：

$$f_k(y,x) = \sum^n_{i=1}f_k(y_{i-1}, y_i, x, i), ;; k=1,2,…,K$$

用$w_k$表示特征$f_k(y,x)$的权值，即：

$$w_k = \left\{\begin{matrix}\lambda_k,\;\;k=1,2,…,K_1\\ \mu_l,\;\;k=K_1+l;l=1,2,…,K_2\end{matrix}\right.$$

于是条件随机场又可以表示成：

$$P(y|x) = \frac{1}{Z(x)}exp\sum^K_{k=1}w_kf_k(y,x)\\Z(x)=\sum_y exp\sum^K_{k=1}w_kf_k(y,x)$$

如果用$w$表示权值向量，即$w=(w_1, …, w_K)^T$，用$F(y,x)$表示全局特征向量，即$F(y,x) = (f_1(y,x),f_2(y,x),…,f_K(y,x))^T$，则条件随机场可以携程向量$w$和$F(y,x)$的内积的形式：
$$P_w(y|x) = \frac{exp(w\cdot F(y,x))}{Z_w(x)}\\Z(x)=\sum_yexp(w\cdot F(y,x))$$

矩阵形式

引入特殊的起点和终点状态标记$y_0=start$，$y_{n+1}=stop$。
对于观测序列$x$的每一个位置$i=1,2,…,n+1$定义$n+1$个$m$阶方阵（$m$是标记$y_i$取值的个数）。

$M_i(x) = [M_i(y_{i-1}, y_i| x)]$
$M_i(y_{i-1}, y_i| x) = exp(W_i(y_{i-1}, y_i| x))$
$W_i(y_{i-1}, y_i| x) = \sum_{k=1}^Kw_kf_k(y_i,y_i,x,i)$

条件随机场的矩阵形式：

$$P_w(y|x) = \frac{1}{Z_w(x)}\prod^{n+1}_{i=1}w_kf_k(y_{i-1},y_i,x,i)\\Z_w(x)=(M_1(x)M_2(x)…M_{n+1}(x))_{start, stop}$$

即，简化了配分函数$Z_w(x)$的计算方式。

三个问题

类似于隐马尔科夫模型（HMM），CRF也有典型的三个问题。对比二者在这三个问题的解决方法的不同，可以更深入理解这两个模型。

1.概率计算问题：给定条件随机场$P(Y|X)$，输入序列$x$和输出序列$y$，计算条件概率$P(Y_i=y_i|x)$和$P(Y_{i-1}=y_{i-1}, Y_i=y_i|x)$和相应的数学期望。
2.学习问题：给定训练数据集，估计条件随机场模型参数，即用极大似然法的方法估计参数。
3.预测问题：给定条件随机场$P(Y|X)$和输入序列（观测序列）$x$，求条件概率最大的输出序列（标记序列）$y^*$。

概率计算问题

给定条件随机场$P(Y|X)$，输入序列$x$和输出序列$y$，计算条件概率$P(Y_i=y_i|x)$和$P(Y_{i-1}=y_{i-1},Y_i=y_i|x)$。

在这里我们可以明显看出，条件随机场直接计算条件概率，因此是判别模型；而HMM先由上一个状态生成下一个状态，再由下一个状态生成下一个输出，因此HMM是生成模型。

类似于HMM，引入前向-后向向量：

对每个下标$i=0,1,…,n+1$，定义前向向量：$\alpha_i(x)$：

$$\alpha_0(y|x) = \left\{\begin{matrix} 1, \;\;y=start\\ 0, \;\;否则\end{matrix}\right.$$

递推公式：

$$\alpha_i^T(y_i|x) = \alpha_{i-1}^T(y_{i-1}|x)M_i(y_{i-1},y_i|x), \;\;i=1,2,…,n+1$$

简单地表示：

$$\alpha_i^T(x) = \alpha_{i-1}^T(x)M_i(x)$$

第$i$个前向向量表示在位置$i$的标记是$y_i$，并且到位置$i$的前部分标记序列的非规范化概率。$y_i$的取值有$m$个，所以$\alpha_i(x)$是$m$维列向量。

类似地，对于每个下标$i=0,1,…,n+1$，定义前后向向量$\beta_i(x)$：

$$\beta_{n+1}(y_{n+1}|x) = \left\{\begin{matrix} 1, \;\;y_{n+1}=stop\ 0, \;\;否则\end{matrix}\right.$$

递推公式：

$$\beta_i(y_i|x) = M_{i+1}(y_i,y_{i+1}|x)\beta_{i+1}(y_{i+1}|x),
\;\;i=1,2,…,n+1$$

简单地表示：

$$\beta_i(x) = M_{i+1}(x)\beta_{i+1}(x)$$

第$i$个后向向量表示在位置$i$的标记是$y_i$，并且从位置$i+1$到$n$的后部分标记序列的非规范化概率。

用前向-后向向量表示配分函数：$Z(x)=\alpha_n^T(x)\cdot 1 = 1^T\cdot\beta_1(x)$

概率计算：

不同于HMM的概率计算，使用前向概率或者后向概率即可，这里计算需要同时使用前向向量和后向向量。

$$P(Y_i=y_i|x) = \frac{\alpha_i^T(y_i|x)\beta_i(y_i|x)}{Z(x)}$$

$$P(Y_{i-1}=y_{i-1}, Y_i=y_i|x) = \frac{\alpha_{i-1}^T(y_{i-1}|x)M_i(y_{i-1}, y_i|x)\beta_i(y_i|x)}{Z(x)}$$

期望值计算：

特征函数$f_k$关于条件分布$P(Y|X)$的期望：

$$E_{P(Y|X)}[f_k] = \sum_yP(y|x)f_k(y, x)\\ = \sum_{i=1}^{n+1}\sum_{y_{i-1}, y_i}f_k(y_{i-1}, y_i, x, i)\frac{\alpha_{i-1}^T(y_{i-1}|x)M_i(y_{i-1}, y_i|x)\beta_i(y_i|x)}{Z(x)}\\k=1,2,..,K$$

特征函数$f_k$关于联合分布$P(X, Y)$的期望：

$$E_{P(X,Y)}[f_k] = \sum_{x,y}P(x,y)\sum_{i=1}^{n+1}f_k(y_{i-1}, y_i, x, i)$$

$$=\sum_x\tilde P(x)\sum_yP(y|x)\sum^{n+1}_{i=1}f_k(y_{i-1}, y, x, i)$$

$$=\sum_x\tilde P(x)\sum_{i=1}^{n+1}\sum_{y_{i-1}y_i}\frac{\alpha_{i-1}^T(y_{i-1}|x)M_i(y_{i-1}, y_i|x)\beta_i(y_i|x)}{Z(x)}$$

$$k=1,2,..,K$$

核心代码：

前向后向和M矩阵都用保存其log值（因为它们本身的值可能很小，计算乘法可能下溢）。

"""
关键变量的尺寸，Y是标注空间的个数，K是特征函数的个数。
all_features:	len(x_vec) + 1, Y, Y, K
log_M_s:
len(x_vec) + 1, Y, Y
log_alphas:		len(x_vec) + 1, Y
log_betas:		len(x_vec) + 1,
Y
log_probs:		len(x_vec) + 1, Y, Y
"""

$M$：

1	log_M_s = np.dot(all_features, w)

前向向量初始化：

1 2	alpha = alphas[0] alpha[start] = 0 # log1 = 0

前向向量的递推公式：

1	alphas[t] = log_dot_vm(alpha, log_M_s[t - 1])

后向向量的初始化：

1 2	beta = betas[-1] beta[end] = 0 # log1 = 0

后向向量的递推公式：

1	betas[t] = log_dot_mv(log_M_s[t], beta)

其中：

def log_dot_vm(loga, logM):
    """通过log向量和log矩阵，计算log(向量^T 点乘 矩阵)"""
return special.logsumexp(np.expand_dims(loga, axis=1) + logM, axis=0)


def
log_dot_mv(logM, logb):
    """通过log向量和log矩阵，计算log(矩阵 点乘 向量)"""
    return
special.logsumexp(logM + np.expand_dims(logb, axis=0), axis=1)

$Z$：

1	log_Z = special.logsumexp(last)

注：special.logsumexp函数等价于np.log(np.sum(np.exp(a), axis))

计算$P(Y_{i-1}=y_{i-1}, Y_i=y_i|x) = \frac{\alpha_{i-1}^T(y_{i-1}|x)M_i(y_{i-1}, y_i|x)\beta_i(y_i|x)}{Z(x)}$：

1
2
3

log_alphas1 = np.expand_dims(log_alphas, axis=2)
log_betas1 = np.expand_dims(log_betas, axis=1)
log_probs = log_alphas1 + log_M + log_betas1 - log_Z

计算特征函数$f_k$关于条件分布$P(Y|X)$的期望：

1	exp_features = np.sum(np.exp(log_probs) * all_features, axis=(0, 1, 2))

特征函数$f_k$关于联合分布$P(X, Y)$的期望：

# y_vec = [START] + y_vec + [END]
yp_vec_ids = y_vec[:-1]
y_vec_ids = y_vec[1:]
emp_features = np.sum(all_features[range(length), yp_vec_ids, y_vec_ids], axis=0)

学习方法

给定训练数据集，估计条件随机场模型参数，即用极大似然法的方法估计参数。

这里学习的参数是$w$，应该对比最大熵的学习算法，HMM的有监督学习的参数估计很简单，参数估计的是三元组概率矩阵。

改进的迭代尺度法

$$L(w) = L_{\tilde P}(P_w)$$

$$ = log\prod_{x,y}P_w(y|x)^{\tilde P(x,y)}$$

$$ = \sum_{x,y}\tilde P(x,y)logP_w(y|x)$$

$$ = \sum_{x,y}[\tilde P(x,y)\sum_{k=1}^Kw_kf_k(x,y)-\tilde P(x,y)logZ_w(x)]$$

$$ = \sum_{j=1}^N\sum_{k=1}^Kw_kf_k(y_j,x_j)-\sum_{j=1}^NlogZ_w(x_j)$$

改进的迭代尺度法引入参数向量的增量向量：$\delta=(\delta_1, …, \delta_K)^T$。

类似于最大熵的迭代尺度法，引入两个方程：

关于转移特征的方程：
- $\sum_{x,y}\tilde P(x,y) \sum_{i=1}^{n+1}t_k(y_{i-1},y_i,x,i)$
- $=\sum_{x,y}\tilde P(x)P(y|x)\sum_{i=1}^{n+1}t_k(y_{i-1},y_i,x,i)exp(\delta_kT(x,y))$
- $k=1,2,…,K_1$
关于状态特征的方程：
- $\sum_{x,y}\tilde P(x,y) \sum_{i=1}^{n+1}s_l(y_{i-1},y_i,x,i)$
- $=\sum_{x,y}\tilde P(x)P(y|x)\sum_{i=1}^{n+1}s_l(y_{i-1},y_i,x,i)exp(\delta_{K_1+l}T(x,y))$
- $l=1,2,…,K_2$
其中：$T(x,y) = \sum_kf_k(y,x) = \sum_{k=1}^K\sum_{i=1}^{n+1}f_k(y_{i-1}, y_i, x, i)$是某数据$(x,y)$出现的所有特征数的总和。

具体算法流程：

输入：特征函数：$t_1,…,t_{K_1}$，$s_1, …, s_{K_2}$；经验分布$\tilde P(x,y)$。
输出：参数估计值$\hat w$；模型$P_{\hat w}$。
1.对于所有的$k \in {1,2,…,K}$，取初始值$w_k=0$
2.对于每一$k \in {1,2,…,K}$：
- a.当$k = 1,2,…,K_1$时，令$\delta_k$是关于转移特征的方程的解；当$k = K_1+l;l=1,…,K_2$时，令$\delta_k$是关于状态特征的方程的解。
- b.更新$w_k$：$w_k\leftarrow w_k+\delta_k$

BFGS算法

梯度函数：$g(w) = \sum_{x,y}\tilde P(x)P_w(y|x)f(x,y) - E_{\tilde P}(f)$

具体算法流程：

输入：特征函数$f_1,…,f_n$；经验分布$\tilde P(x,y)$。
输出：参数估计值$\hat w$；模型$P_{\hat w}$。
1.选定初始点$w^{(0)}$，取$B_0$是正定对称矩阵，置$k=0$。
2.计算$g_k=g(w^{(k)})$，若$g_k=0$，则停止计算，否则转步骤3。
3.由$B_kp_k=-g_k$，求出$p_k$
4.一维搜索：求$\lambda_k$使得：$f(w^{(k)}+\lambda_kp_k) = min_{\lambda\geq 0}f(w^{(k)}+\lambda p_k)$
5.置$g_{k+1} = g(w^{(k+1)})$，若$g_k=0$，则停止计算；否则，求$B_{k+1}$：$B_{k+1}=B_k+\frac{y_kt_k^T}{y_k^T\delta_k}-\frac{B_k\delta_k\delta_k^TB_k}{\delta_k^tB_k\delta_k}$，其中，$y_k = g_{k+1}-g_k$，$\delta_k = w^{(k+1)-w^{(k)}}$
7.置$k=k+1$，转到步骤3。

关键代码：

似然函数：

1	likelihood += np.sum(log_M_s[range(length), yp_vec_ids, y_vec_ids]) - log_Z

训练，直接使用scipy中的optimize.fmin_l_bfgs_b去优化似然函数：

def train(self, x_vecs, y_vecs, debug=False):
    vectorised_x_vecs, vectorised_y_vecs = self.create_vector_list(x_vecs, y_vecs)
    l = lambda w: self.neg_likelihood_and_deriv(vectorised_x_vecs, vectorised_y_vecs, w)
    val = optimize.fmin_l_bfgs_b(l, self.w)
    if debug:
        print(val)
    self.w, _, _ = val
    return self.w

optimize.fmin_l_bfgs_b的第一个参数是被优化的目标函数，这个函数需要返回函数值和梯度值，梯度值的计算：

1	derivative += emp_features - exp_features

即特征关于模型的训练数据的期望和关于模型的期望的差。

预测算法

给定条件随机场$P(Y|X)$和输入序列（观测序列）$x$，求条件概率最大的输出序列（标记序列）$y^*$，即，对观测序列进行标注。
类似于HMM，CRF也是采用维特比算法进行预测。

$$y^* = max_y(w\cdot F(y,x))$$

$$w=(w_1,…,w_K)^T$$

$$F(y,x)=(f_1(y,x), …, f_K(y,x))^T$$

$$f_k(y,x) =\sum_{i=1}^nf_k(y_{i-1}, y_i, x, i), k=1,2,…,K$$

注意，这里只用计算非规范化概率，即不用计算配分函数$Z$，可以大大提高效率。

具体算法流程：

输入：模型特征向量$F(y,x)$和权值向量$w$，观测序列$x=(x_1,…,x_n)$；
输出：最优路径$y^*=(y_1^*, y_2^*, …, y_n^*)$
1.初始化非规范化概率：$\delta_1(j) = w\cdot F_1(y_0=start, y_1=j, x), \;\;\;j=1,…,m$
2.递推：对$i=1,2,…,n$：
- $\delta_i(l) = max_{1\leq j \leq m}{\delta_{i-1}(j) + w\cdot F_i(y_{i-1}=j,y_i=l, x);;;l=1,2,…,m}$
- 对应的路径：$\Psi_i(l) = argmax_{1\leq j \leq m}{\delta_{i-1}(j) + w\cdot F_i(y_{i-1}=j,y_i=l, x)\;\;\;l=1,2,…,m}$
3.终止：
- $max_y(w\cdot F(y,x)) = max_{1\leq j \leq m}\delta_n(j)$
- $y^*_n = argmax_{1\leq j \leq m}\delta_n(j)$
4.返回路径：$y_i^* = \Psi_{i+1}(y_{i+1}^*), \;\;i=n-1,n-2,…,1$

核心代码：

def predict(self, x_vec, debug=False):
    """给定x，预测y。使用Viterbi算法"""
    # all_features, len(x_vec) + 1, Y, Y, K
    all_features = self.get_all_features(x_vec)
    # log_potential: len(x_vec) + 1, Y, Y  保存各个下标的非规范化概率
    log_potential = np.dot(all_features, self.w)
    T = len(x_vec)
    Y = len(self.labels)
    # Psi保存每个时刻最优情况的下标
    Psi = np.ones((T, Y), dtype=np.int32) * -1
    # 初始化
    delta = log_potential[0, 0]
    # 递推
    for t in range(1, T):
        next_delta = np.zeros(Y)
        for y in range(Y):
            w = delta + log_potential[t, :, y]
            Psi[t, y] = psi = w.argmax()
            next_delta[y] = w[psi]
        delta = next_delta
    # 回溯找到最优路径
    y = delta.argmax()
    trace = []
    for t in reversed(range(T)):
        trace.append(y)
        y = Psi[t, y]
    trace.reverse()
    return [self.labels[i] for i in trace]

完整代码地址：https://github.com/applenob/simple_crf