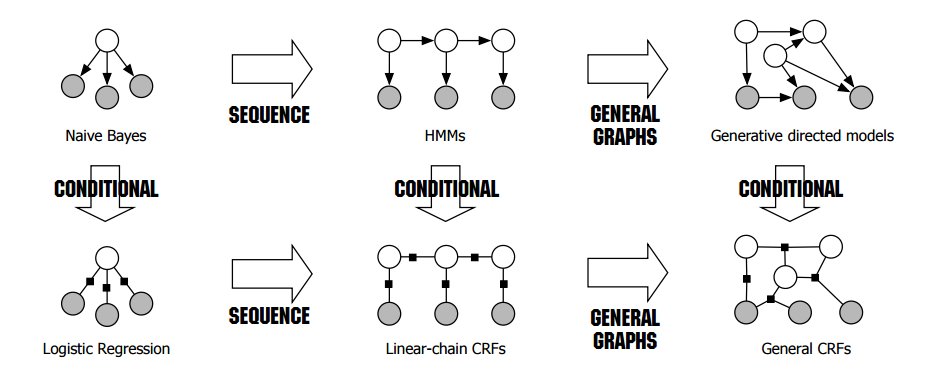
Logistic Regression VS Max Entropy 和 Theano实现

Posted on Edited on In

动机

首先，来说说为什么要写LR和ME。最近在研究《 An Introduction to Conditional Random Fields for Relational Learning》，发现了一张神图。

稍微解释一下：我们把机器学习模型分为两类，一类是生成模型，一类是判别模型。第一行的都是生成模型，第二行的都是判别模型。所谓生成模型是通过建模$P(x,y)$，判别模型是直接建模$P(y|x)$。把这两种建模思维和图模型相结合，我们可以描述随机变量之间的关系，使得模型变得复杂。一般这些随机变量是同一类型的在不同时间序列上的变量，具体关系由图模型描述。

从图上看，关系最简单的，是朴素贝叶斯模型和LR(ME)模型。这里把LR和ME归为了一类，这是因为LR和ME在本质上是等价的（虽然他们的建模思想完全不同），都是属于对数线性模型，也都是判别模型。朴素贝叶斯很简单了，就不多说了，LR和ME却还可以引申出很多知识点，比如拉格朗日对偶，最优化方法。这些都在后面的博文中详细描述。这里专注把LR和ME的思路理清，以及它们背后的intuition。最后使用Theano实现。

Logistic Regression

首先，直接给出Logistic Regression的模型：

$$P(Y=1|x)=\frac{exp(w\cdot x)}{1+exp(w\cdot x)}$$
$$P(Y=0|x)=\frac{1}{1+exp(w\cdot x)}$$

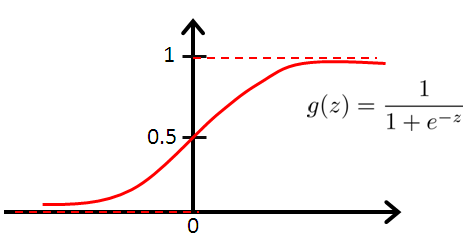
好吧，肯定有人觉得不高兴了这个模型难道是凭空而来的吗？当然不是，给你看个图：

这个就是传说中的Logistic函数，和我们模型的表达式是不是一毛一样？

如果我们把$w\cdot x$理解成evidence，那么当我们获得evidence的时候，我想知道数据是否是属于某个类，我们把他扔进Logistic函数，就会出来一个0-1的值。evidence在某个范围的时候这个值，就会趋近于0，evidence在另外一个范围的时候，它就会趋近1，那这个值其实就可以认为是原始数据是否属于某个类的概率。

以上，就是Logistic Regression的intuition。

OK，有了模型的表达式，接下来要估计模型的参数了。

很自然的，我们想到了极大似然估计参数。

对数似然函数：
$$L(w)=log(\prod^N_{i=1}[π(x_i)]^{y_i}[1-π(x_i)]^{1-y_i})$$

$$=\sum^N_{i=1}[y_ilogπ(x_i)+(1-y_i)log(1-π(x_i))]$$

$$=\sum^N_{i=1}[y_ilog\frac{π(x_i)}{1-π(x_i)}+log(1-π(x_i))]$$

$$=\sum^N_{i=1}[y_i(w\cdot x_i)-log(1+exp(w\cdot x_i))]$$

其中: $π(x_i)=P(Y=1|x_i)$

算到这一步，就变成了最优化问题，对L(w)求极大值，得到w的估计值。具体的最优化求解过程，这篇文章暂且不提。

Max Entropy

最大熵模型并不像LR一样，一上来就给了模型的表达式，需要从最基础的最大熵思想，去推出表达式。

所谓的最大熵，就是指，当我们对一个分布一无所知的时候，我们认为这个分布是均匀分布的。当然这只是最大熵的一个结果。

这里最大熵最大化的，是条件熵H(Y|X)。

$$H(Y|X)=-\sum_{x,y}\hat{P}(x)P(y|x)logP(y|x)$$
具体的关于信息熵的文章，可以看colah的这篇博客，里面对信息熵/互信息/条件熵的物理意义做很好的解释。

好的，我们的最大熵有了目标函数，那么约束条件是什么？

首先引入特征函数：

特征函数f(x,y)关于经验分布$\hat P(x,y)$的期望：

$$E_{\hat P}(f)=\sum_{x,y}\hat P(x,y)f(x,y)$$
特征函数f(x,y)关于模型P(Y|X)与经验分布$\hat P(x,y)$的期望：

$$E_{P}(f)=\sum_{x,y}\hat P(x)P(y|x)f(x,y)$$

我们希望，模型在训练完以后，能够获取到训练数据中的信息。这样的想法，用上面的两个期望表达，就是：

$$E_{\hat P}(f)=E_{P}(f)$$

给定了目标函数和约束条件，我们通过拉格朗日对偶法，解得模型的表达式，（具体的求解过程省略，这里主要是展现模型思想）：

$$P_w(y|x)=\frac{1}{Z_w(x)}exp\bigl(\begin{smallmatrix} \sum_{i=1}^{n} w_i\cdot f_i(x,y) \end{smallmatrix}\bigr)$$

其中，$Z_w(x)$是归一化因子，$Z_w(x)=\sum_yexp\bigl(\begin{smallmatrix}\sum_{i=1}^{n} w_i\cdot f_i(x,y) \end{smallmatrix}\bigr)$

接下来，和LR一样，使用极大似然法估计参数，将问题转化为最优化问题。

实现

这里使用Theano实现了几种LR和ME，为什么使用Theano只是因为可以使用Theano的自动求导，而且最近项目也在看Theano的代码，比较熟悉。

1
2
3
4
5
6
import numpy
import theano
import theano.tensor as T
def calc_acu(label, predict):
    comp = [1 if l==pre else 0 for l, pre in zip(label, predict)]
    return float(sum(comp))/len(comp)
1
Using gpu device 0: GeForce GTX 960M (CNMeM is disabled, cuDNN not available)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
"""
code from http://deeplearning.net/software/theano/tutorial/examples.html
"""
rng = numpy.random

N = 400                                  # training sample size
feats = 784                               # number of input variables

# generate a dataset: D = (input_values, target_class)
D = (rng.randn(N, feats), rng.randint(size=N, low=0, high=2))
training_steps = 10000

# Declare Theano symbolic variables
x = T.dmatrix("x")
y = T.dvector("y")

# initialize the weight vector w randomly
#
# this and the following bias variable b
# are shared so they keep their values
# between training iterations (updates)
w = theano.shared(rng.randn(feats), name="w")

# initialize the bias term
b = theano.shared(0., name="b")

# print("Initial model:")
# print(w.get_value())
# print(b.get_value())

# Construct Theano expression graph
p_1 = 1 / (1 + T.exp(-T.dot(x, w) - b))   # Probability that target = 1
prediction = p_1 > 0.5                    # The prediction thresholded
xent = -y * T.log(p_1) - (1-y) * T.log(1-p_1) # Cross-entropy loss function
cost = xent.mean() + 0.01 * (w ** 2).sum()# The cost to minimize
gw, gb = T.grad(cost, [w, b])             # Compute the gradient of the cost
                                          # w.r.t weight vector w and
                                          # bias term b
                                          # (we shall return to this in a
                                          # following section of this tutorial)

# Compile
train = theano.function(
          inputs=[x,y],
          outputs=[prediction, xent],
          updates=((w, w - 0.1 * gw), (b, b - 0.1 * gb)))
predict = theano.function(inputs=[x], outputs=prediction)

# Train
for i in range(training_steps):
    pred, err = train(D[0], D[1])

# print("Final model:")
# print(w.get_value())
# print(b.get_value())
print("target values for D:")
print(D[1])
print("prediction on D:")
print(predict(D[0]))
print("accuracy:")
print(calc_acu(D[1], predict(D[0])))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
target values for D:
[1 0 0 1 0 0 1 1 0 1 0 1 1 1 1 1 1 0 0 0 0 1 0 1 0 0 1 0 0 0 1 1 1 0 0 1 1
 0 0 0 0 1 0 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 0 1 1 1 0 1 0 0 0 0 1 1 1 0 0 1
 1 0 0 0 0 0 1 0 0 0 1 1 1 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 1 0 0 0 0 0 1 1
 1 1 1 0 1 0 0 1 0 0 0 0 1 1 0 0 1 1 0 1 0 0 0 0 0 1 1 0 1 0 0 0 0 1 1 1 1
 0 0 1 0 0 0 1 0 1 0 1 1 0 1 0 0 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 0 1 0 0 1 0
 1 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 0 0 0 0 1 0 1 1 0 0 0 1 0 0 1 1 1 0 0 1
 1 0 1 0 1 0 0 0 1 0 0 1 0 1 1 1 1 0 1 0 0 1 0 0 1 1 1 0 1 0 0 0 1 0 0 1 1
 1 0 0 0 1 1 1 1 1 1 0 0 0 1 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 1 0 1 1 1 1 1
 0 0 0 1 1 1 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 1
 1 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 1 0 1 1 1 0 0 0 0 1 1 0 1 1 1 0
 1 1 0 0 1 0 0 1 0 1 0 1 1 1 1 0 1 1 1 0 0 0 0 0 0 1 1 0 1 1]
prediction on D:
[1 0 0 1 0 0 1 1 0 1 0 1 1 1 1 1 1 0 0 0 0 1 0 1 0 0 1 0 0 0 1 1 1 0 0 1 1
 0 0 0 0 1 0 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 0 1 1 1 0 1 0 0 0 0 1 1 1 0 0 1
 1 0 0 0 0 0 1 0 0 0 1 1 1 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 1 0 0 0 0 0 1 1
 1 1 1 0 1 0 0 1 0 0 0 0 1 1 0 0 1 1 0 1 0 0 0 0 0 1 1 0 1 0 0 0 0 1 1 1 1
 0 0 1 0 0 0 1 0 1 0 1 1 0 1 0 0 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 0 1 0 0 1 0
 1 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 0 0 0 0 1 0 1 1 0 0 0 1 0 0 1 1 1 0 0 1
 1 0 1 0 1 0 0 0 1 0 0 1 0 1 1 1 1 0 1 0 0 1 0 0 1 1 1 0 1 0 0 0 1 0 0 1 1
 1 0 0 0 1 1 1 1 1 1 0 0 0 1 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 1 0 1 1 1 1 1
 0 0 0 1 1 1 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 1
 1 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 1 0 1 1 1 0 0 0 0 1 1 0 1 1 1 0
 1 1 0 0 1 0 0 1 0 1 0 1 1 1 1 0 1 1 1 0 0 0 0 0 0 1 1 0 1 1]
accuracy:
1.0

上面的代码使用了交叉熵作为cost function，并没有使用最大似然估计。最优化方法是最简单的梯度下降法。

下面使用极大似然估计参数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
x = T.dmatrix("x")
y = T.dvector("y")
w = theano.shared(rng.randn(feats), name="w")
b = theano.shared(0., name="b")
# Construct Theano expression graph
p_1 = T.exp(T.dot(x, w) + b) / (1 + T.exp(T.dot(x, w) + b))   
prediction = p_1 > 0.5                    
# 最大似然函数，即新的优化目标
L_w = y*(T.dot(x, w) + b) - T.log(1 + T.exp(T.dot(x, w) + b))
goal = L_w.sum()
gw, gb = T.grad(goal, [w, b])             

# Compile
# 由于是最大化，需要从梯度下降，改成梯度上升
train = theano.function(
          inputs=[x,y],
          outputs=[prediction,L_w],
          updates=((w, w + 0.1 * gw), (b, b + 0.1 * gb)))
predict = theano.function(inputs=[x], outputs=prediction)

# Train
for i in range(training_steps):
    pred, goal = train(D[0], D[1])
    
# 输出训练集上的预测结果
print("target values for D:")
print(D[1])
print("prediction on D:")
print(predict(D[0]))
print("accuracy:")
print(calc_acu(D[1], predict(D[0])))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
target values for D:
[1 0 0 1 0 0 1 1 0 1 0 1 1 1 1 1 1 0 0 0 0 1 0 1 0 0 1 0 0 0 1 1 1 0 0 1 1
 0 0 0 0 1 0 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 0 1 1 1 0 1 0 0 0 0 1 1 1 0 0 1
 1 0 0 0 0 0 1 0 0 0 1 1 1 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 1 0 0 0 0 0 1 1
 1 1 1 0 1 0 0 1 0 0 0 0 1 1 0 0 1 1 0 1 0 0 0 0 0 1 1 0 1 0 0 0 0 1 1 1 1
 0 0 1 0 0 0 1 0 1 0 1 1 0 1 0 0 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 0 1 0 0 1 0
 1 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 0 0 0 0 1 0 1 1 0 0 0 1 0 0 1 1 1 0 0 1
 1 0 1 0 1 0 0 0 1 0 0 1 0 1 1 1 1 0 1 0 0 1 0 0 1 1 1 0 1 0 0 0 1 0 0 1 1
 1 0 0 0 1 1 1 1 1 1 0 0 0 1 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 1 0 1 1 1 1 1
 0 0 0 1 1 1 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 1
 1 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 1 0 1 1 1 0 0 0 0 1 1 0 1 1 1 0
 1 1 0 0 1 0 0 1 0 1 0 1 1 1 1 0 1 1 1 0 0 0 0 0 0 1 1 0 1 1]
prediction on D:
[1 0 0 1 0 0 1 1 0 1 0 1 1 1 1 1 1 0 0 0 0 1 0 1 0 0 1 0 0 0 1 1 1 0 0 1 1
 0 0 0 0 1 0 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 0 1 1 1 0 1 0 0 0 0 1 1 1 0 0 1
 1 0 0 0 0 0 1 0 0 0 1 1 1 1 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 1 0 0 0 0 0 1 1
 1 1 1 0 1 0 0 1 0 0 0 0 1 1 0 0 1 1 0 1 0 0 0 0 0 1 1 0 1 0 0 0 0 1 1 1 1
 0 0 1 0 0 0 1 0 1 0 1 1 0 1 0 0 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 0 1 0 0 1 0
 1 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 0 0 0 0 1 0 1 1 0 0 0 1 0 0 1 1 1 0 0 1
 1 0 1 0 1 0 0 0 1 0 0 1 0 1 1 1 1 0 1 0 0 1 0 0 1 1 1 0 1 0 0 0 1 0 0 1 1
 1 0 0 0 1 1 1 1 1 1 0 0 0 1 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 1 0 1 1 1 1 1
 0 0 0 1 1 1 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 1
 1 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 1 0 1 1 1 0 0 0 0 1 1 0 1 1 1 0
 1 1 0 0 1 0 0 1 0 1 0 1 1 1 1 0 1 1 1 0 0 0 0 0 0 1 1 0 1 1]
accuracy:
1.0

Reference

  • 《统计学习方法》李航