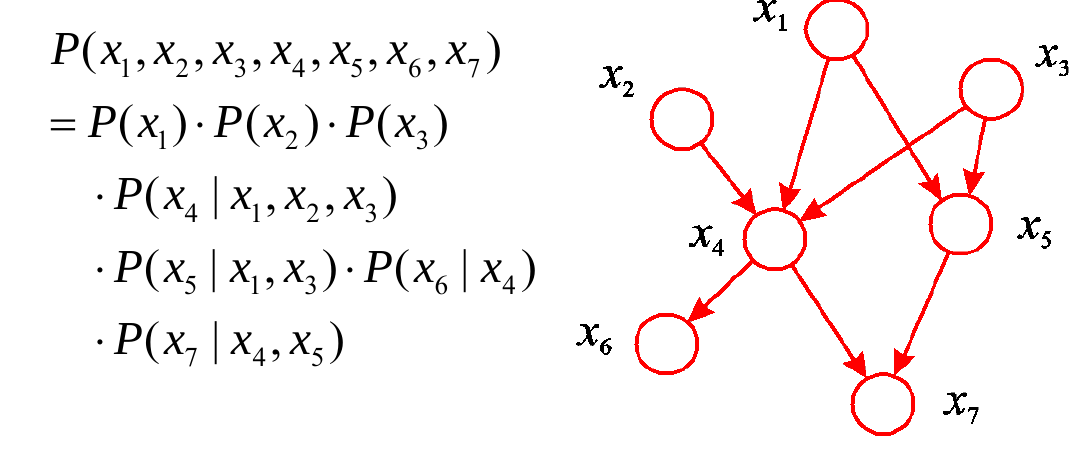
图模型的引入
首先总结一下图模型,所谓图模型,其实就是在统计建模的时候,结合图论的思想。
$图模型=概率论+图论$
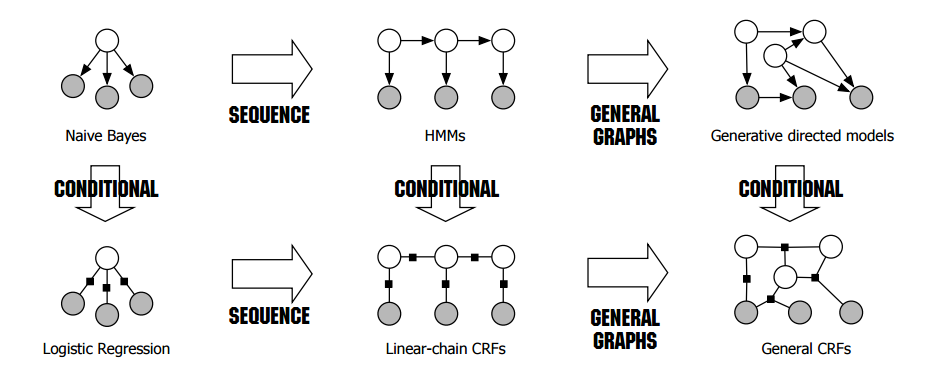
让我们先从朴素贝叶斯开始思考,随机变量$y$和所有的观测变量$X$有关,但每个观测变量对于$y$来说,又是独立的,也就是我们说的“naive”。
这基本上是最简单的随机变量的关系了:$P(X|y)=p(x_1|y)\cdot p(x_2|y)…\cdot p(x_n|y)$。
那我们可以从这里引申出什么呢?如果把所有的随机变量,都用图论中的节点表示,变量间的关系,由边表示,暂时先不考虑边的方向的问题,那么朴素贝叶斯就可以很直观地画成上面的第一幅图。
再来回忆一下最大熵。最大熵的建模思想并不是来源于图论,但是看看最大熵模型的表达式:
$$P_w(y|x)=\frac{1}{Z_w(x)}exp\bigl(\begin{smallmatrix} \sum_{i=1}^{n} w_i\cdot f_i(x,y) \end{smallmatrix}\bigr)$$
我们换一个思路去想:特征函数$f_i(x,y)$刻画的是变量$x$和$y$之间的关系,这跟朴素贝叶斯中的条件概率不同,条件概率是单向的,$p(y|x)!=p(x|y)$,而特征函数是双向的,或者说是无向的,$f(x,y)=f(y,x)$。因此为了区分这二者的区别我们把图模型分为有向图和无向图模型两种。
下面给出二者更加规范的定义(来自:An introduction to conditional random fields):
无向图
考虑一系列随机变量$Y$,$s∈1,2,…|Y|$。$y$是$Y$的分布。
认为$y$的概率分布可以表示成一系列和$Y$有关的因素(factor)的乘积。这个因素的形式是:$\Psi_a(y_a)$,$a∈1,2,…,A$。
加粗代表是向量。
$$p(\mathbf{y})=\frac{1}{Z}\prod_{a=1}^{A}\Psi_a(\mathbf{y}_a)$$
其中$Z$是归一化因子。
例:
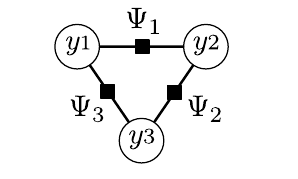
$$p(y_1,y_2,y_3)\propto \Psi_1(y_1,y_2) \Psi_2(y_2,y_3) \Psi_3(y_3,y_1)$$
有向图
$G$是一个DAG(有向无环图),$π(s)$是$Y_s$的下标,DAG的模型可以这么理解:联合概率分布等于每个节点在它们的父节点的条件下的条件概率的累乘,写成:
$$p(\mathbf{y})=\prod^S_{s=1}p(y_s|\mathbf{y}_{π(s)})$$
例: