迁移学习入门
迁移学习简单地说,首先有个目标任务$T$,目标数据$D_T$数据量偏小,此时有一个相似的源任务$S$,源数据$D_S$相对更充分,迁移学习的目标即如何借助源任务去提高目标任务的效果。
第四范式的罗远升有一篇很不错的文章《迁移学习实战:从算法到实践》,看了那篇文章,你会对迁移学习有个大概的认识。
迁移学习方法分类
根据所要迁移的知识的表示形式(即“What to transfer”),分为以下四大类:
- 基于样本的迁移学习(instance-transfer);
- 基于参数的迁移学习(parameter-transfer);
- 基于特征表示的迁移学习(feature- representation-transfer);
- 基于关系知识的迁移(relation-knowledge-transfer)。
基于样本的迁移学习
所谓基于样本,就是从源数据中选取对目标领域建模有帮助的样本。这样操作就有一个前提假设:源领域和目标领域的特征空间和目标空间要一致。
TrAdaBoost
TrAdaBoost是一个典型的基于样本的迁移学习算法。关于基础的AdaBoost可以看之前写的博客。
TrAdaBoost的思想是:
- 当一个目标数据$D_T$中的样本被错误的分类之后,可以认为这个样本是很难分类的,因此增大这个样本的权重,这样在下一次的训练中这个样本所占的比重变大,这一点和基本的AdaBoost算法的思想是一样的;
- 如果源数据$D_S$中的一个样本被错误的分类了,可以认为这个样本对于目标数据是不同的,因此降低这个样本的权重,降低这个样本在分类器中所占的比重。
TrAdaBoost算法:
- 先规定源数据:$D_S=(x_i^s, c(x_i^s))$,样本个数为$n$,目标数据:$D_T=(x_i^t, c(x_i^t))$,样本个数为$m$,测试数据:$S = {(x_i^{test})}$。
- 输入:训练集$D_S$和$D_T$,测试集$S$,一个基本分类器Learner,迭代次数N。
- 1.初始化:
- 初始化权重向量:
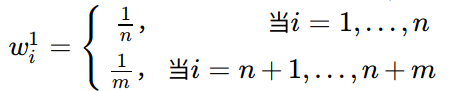
- 设置$\beta = 1/(1+\sqrt{2\ln{n/N}})$
- 初始化权重向量:
- 2.$For;t = 1, …, N$:
- 3.归一化的权重:$\mathbf p^t = \frac{\mathbf w^t}{\sum_{i=1}^{n+m}w_i^t}$;
- 4.使用带权重的两个训练数据训练Learner,得到在$S$上的分类器$h_t:X\rightarrow Y$;
- 5.计算$h_t$在$D_T$中的错误率:$\epsilon_t = \sum_{i=n+1}^{n+m}\frac{w_i^t|h_t(x_i)-c(x_i)|}{\sum_{i=n+1}^{n+m}w_i^t}$;
- 6.令$\beta_t = \epsilon_t(1-\epsilon_t)$,**更新权重向量(重点)**:
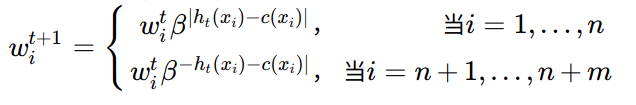
基于参数的迁移学习
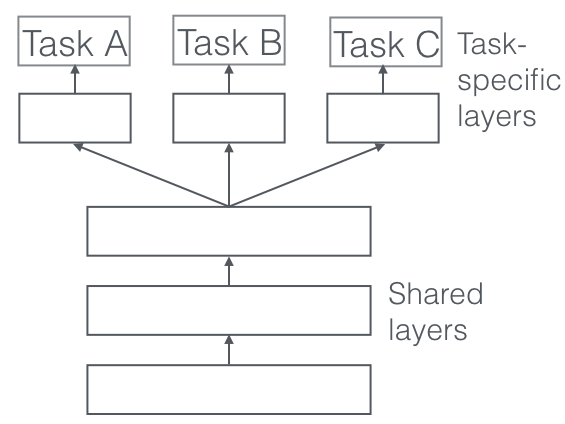
基于参数就是源任务和目标任务使用同一个模型,并且共享参数。典型的方法:多任务学习(multi-task learning)。
基于特征表示的迁移学习
基于特征表示的迁移学习是指利用源数据学会一个特征表示的方法,再用这个方法去提取目标数据的特征。
根据特征表示学习方法的不同也可以分为有监督和无监督两类。