这篇博客中,我通过学习hankcs 的Java版本,自己试着做一个简单的Python版本,用于学习和理清思路。
思路 所谓生成式句法解析是指生成一些列依存句法树,挑出概率最大的一棵。
这里的实现考虑了词性信息+词汇信息,使用最大生成树Prim算法搜索最终结果,实现一个简单的汉语依存句法分析器。
具体:
训练:
统计词语$WordA$和词语$WordB$构成依存关系$DrC$的频次。
统计词语$WordA$和词性$TagB$构成依存关系$DrD$的频次。
统计词性$TagA$和词语$WordB$构成依存关系$DrE$的频次。
统计词性$TagA$和词性$TagB$构成依存关系$DrF$的频次。
解析:
为句子中的词语$i$和词语$j$生成多条依存句法边,权值是上面4中频次的综合。
取边的权值最大的作为唯一的边,加入有向图。
使用Prim最大生成树算法,计算出最大生成树,格式化输出。
数据 使用第二届自然语言处理与中文计算会议(NLP&CC 2013)清华大学的数据。
下载地址:http://tcci.ccf.org.cn/conference/2013/dldoc/evsam05.zip
这些树库语料都是CoNLL格式的,CoNLL格式的语料以.conll结尾:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 CONLL标注格式包含10列,分别为: ——————————————————————————— ID FORM LEMMA CPOSTAG POSTAG FEATS HEAD DEPREL PHEAD PDEPREL ——————————————————————————— 本次评测只用到前8列,其含义分别为: 1 ID 当前词在句子中的序号,1开始. 2 FORM 当前词语或标点 3 LEMMA 当前词语(或标点)的原型或词干,在中文中,此列与FORM相同 4 CPOSTAG 当前词语的词性(粗粒度) 5 POSTAG 当前词语的词性(细粒度) 6 FEATS 句法特征,在本次评测中,此列未被使用,全部以下划线代替。 7 HEAD 当前词语的中心词 8 DEPREL 当前词语与中心词的依存关系 在CONLL格式中,每个词语占一行,无值列用下划线'_'代替,列的分隔符为制表符'\t',行的分隔符为换行符'\n';句子与句子之间用空行分隔。
模型训练 这里所谓的模型训练即统计之前说的四种词频。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 from collections import namedtupletrain_file_name = "../data/evsam05/tree/THU/train.conll" ConllRow = namedtuple("ConllRow" , ["ID" , "FORM" , "LEMMA" , "CPOSTAG" , "POSTAG" , "FEATS" , "HEAD" , "DEPREL" ]) def add_to_dict (d, k, dep ): if k not in d: d[k] = {dep: 1 } elif dep not in d[k]: d[k][dep] = 1 else : d[k][dep] += 1 c_dict = {} d_dict = {} e_dict = {} f_dict = {} count = 0 with open (train_file_name) as f: sentence = [] for line in f: if line == "\n" : count += len (sentence) for row in sentence: if int (row.HEAD) != 0 : add_to_dict(c_dict, (row.LEMMA, sentence[int (row.HEAD)-1 ].LEMMA), row.DEPREL) add_to_dict(d_dict, (row.LEMMA, sentence[int (row.HEAD)-1 ].CPOSTAG), row.DEPREL) add_to_dict(e_dict, (row.CPOSTAG, sentence[int (row.HEAD)-1 ].LEMMA), row.DEPREL) add_to_dict(f_dict, (row.CPOSTAG, sentence[int (row.HEAD)-1 ].CPOSTAG), row.DEPREL) else : add_to_dict(c_dict, (row.LEMMA, "Root" ), "Root" ) add_to_dict(d_dict, (row.LEMMA, "Root" ), "Root" ) add_to_dict(e_dict, (row.CPOSTAG, "Root" ), "Root" ) add_to_dict(f_dict, (row.CPOSTAG, "Root" ), "Root" ) sentence = [] else : sentence.append(ConllRow._make(line.replace("\n" , "" ).strip().split("\t" )))
1 list (c_dict.items())[:10 ]
1 2 3 4 5 6 7 8 9 10 [(('坚决', '惩治'), {'方式': 1}), (('惩治', 'Root'), {'Root': 3}), (('贪污', '犯罪'), {'限定': 17}), (('贿赂', '贪污'), {'连接依存': 37}), (('等', '贪污'), {'连接依存': 34}), (('经济', '犯罪'), {'限定': 19}), (('犯罪', '惩治'), {'受事': 3}), (('最高', '检察院'), {'限定': 2}), (('人民', '检察院'), {'限定': 3}), (('检察院', '检察长'), {'限定': 2})]
1 2 3 4 5 6 7 8 9 10 11 def calc_dict_size (one_dict ): count = 0 for v_dict in one_dict.values(): for k, v in v_dict.items(): count += v return count cc = calc_dict_size(c_dict) dc = calc_dict_size(d_dict) ec = calc_dict_size(e_dict) fc = calc_dict_size(f_dict) print (cc, dc, ec, fc)
1 165534 165534 165534 165534
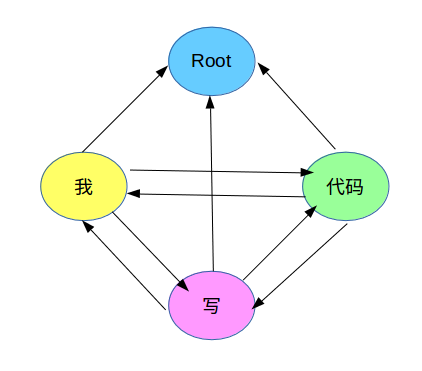
构建图 进来一句句子,首先要做分词 和词性判断 。
然后在句首加入root,对一句有$n$个词的句子,两两之间可能有$(n+1)×n-n$条有向边。
这里的箭头是指向被依赖的HEAD。
有向边的权值计算方法:
$$没有的话取\;\; log(词到词性依存关系数/总数) *10$$
$$没有的话取\;\; log(词性到词依存关系数/总数) *10$$
$$没有的话取\;\;log(词性到词性依存关系数/总数) *100$$
解释:第一种情况的权值要最大,第二第三种稍小,第四种最小。注意这里log计算后是负数。
1 2 3 4 5 6 7 8 import jiebaimport jieba.possegimport numpy as nptest_sen = "我写代码" seg_list = list (jieba.posseg.cut(test_sen)) seg_list
1 [pair('我', 'r'), pair('写', 'v'), pair('代码', 'n')]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 def get_max_from_dict (one_dict, k ): return sorted (one_dict[k].items(), key=lambda i: i[1 ], reverse=True )[0 ] def calc_edge_name_and_weight (pair_1, pair_2 ): if (pair_1.word, pair_2.word) in c_dict: name, num = get_max_from_dict(c_dict, (pair_1.word, pair_2.word)) return name, np.log(float (num)/count) elif (pair_1.word, pair_2.flag) in d_dict: name, num = get_max_from_dict(d_dict, (pair_1.word, pair_2.flag)) return name, np.log(float (num)/count) elif (pair_1.flag, pair_2.word) in e_dict: name, num = get_max_from_dict(e_dict, (pair_1.flag, pair_2.word)) return name, np.log(float (num)/count) elif (pair_1.flag, pair_2.flag) in f_dict: name, num = get_max_from_dict(f_dict, (pair_1.flag, pair_2.flag)) return name, np.log(float (num)/count) return "" , -9999 Edge = namedtuple("Edge" , ["name" , "weight" , "from_id" , "to_id" ]) root_pair = jieba.posseg.pair("Root" , "Root" ) graph_edges = [] for i, pair_1 in enumerate (seg_list): for j, pair_2 in enumerate (seg_list): if pair_1 != pair_2: graph_edges.append(Edge._make(calc_edge_name_and_weight(pair_1, pair_2) + (i+1 , j+1 ))) graph_edges
1 2 3 4 5 6 [Edge(name='施事', weight=-11.323784710206265, from_id=1, to_id=2), Edge(name='限定', weight=-7.7974241855901036, from_id=1, to_id=3), Edge(name='连接依存', weight=-10.9183196020981, from_id=2, to_id=1), Edge(name='内容', weight=-10.63063752964632, from_id=2, to_id=3), Edge(name='连接依存', weight=-11.323784710206265, from_id=3, to_id=1), Edge(name='内容', weight=-8.8814376748370609, from_id=3, to_id=2)]
1 2 3 4 root_edges = [] for i, one_pair in enumerate (seg_list): root_edges.append(Edge._make(calc_edge_name_and_weight(one_pair, root_pair) + (i, 0 ))) root_edges
1 2 3 [Edge(name='Root', weight=-12.016931890766211, from_id=0, to_id=0), Edge(name='Root', weight=-8.8814376748370609, from_id=1, to_id=0), Edge(name='Root', weight=-4.318902720493405, from_id=2, to_id=0)]
Prim算法 Prim核心思路 :任意挑一个顶点,添加权值最大边,直至所有顶点都在树中,得到一棵最大生成树。
1 2 3 tree_edges = [] tree_edges.append(sorted (root_edges, key=lambda e: e.weight, reverse=True )[0 ]) tree_edges
1 [Edge(name='Root', weight=-4.318902720493405, from_id=2, to_id=0)]
1 2 3 4 nodes = set ([tree_edges[0 ].from_id]) target_nodes = set (range (1 , len (seg_list)+1 )) print (nodes)target_nodes
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 new_sorted = sorted (graph_edges, key=lambda e: e.weight, reverse=True ) while nodes != target_nodes: cut_id = -1 for i, one_edge in enumerate (new_sorted): if one_edge.from_id in nodes and one_edge.to_id in target_nodes - nodes: nodes.add(one_edge.to_id) tree_edges.append(one_edge) cut_id = i break elif one_edge.to_id in nodes and one_edge.from_id in target_nodes - nodes: nodes.add(one_edge.from_id) tree_edges.append(one_edge) cut_id = i break if cut_id != -1 : del new_sorted[cut_id] new_sorted = sorted (new_sorted, key=lambda e: e.weight, reverse=True )
1 2 3 [Edge(name='Root', weight=-4.318902720493405, from_id=2, to_id=0), Edge(name='内容', weight=-8.8814376748370609, from_id=3, to_id=2), Edge(name='限定', weight=-7.7974241855901036, from_id=1, to_id=3)]
注意到这里的实现是从DEP指向HEAD,所以和一般常用的箭头方向正好相反,下面的函数中将顺序反过来,并输出标准的CONLL格式
1 2 3 4 5 6 7 8 9 def edges2conll (edges, seg_list ): for i, pair in enumerate (seg_list): head = -1 name = "" for one_edge in edges: if one_edge.from_id == i + 1 : head = one_edge.to_id name = one_edge.name print ("\t" .join([str (i + 1 ), pair.word, pair.word, pair.flag, pair.flag, "_" , str (head), name, "_" , "_" ]))
1 edges2conll(tree_edges, seg_list)
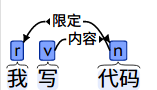
1 2 3 1 我 我 r r _ 3 限定 _ _ 2 写 写 v v _ 0 Root _ _ 3 代码 代码 n n _ 2 内容 _ _
使用这个在线可视化工具:http://spyysalo.github.io/conllu.js/ ,输入conll格式的数据可视化一下:
果然还是个Toy,三个错了一个。
总结 这只是我学习Hank写的一个小demo,主要目的是学习简单的依存解析器的实现原理。
缺点:prim算法会产生交叉弧,prim本身的实现也不是最优的,还有很多地方需要改进,也没有进行测评。