N-最短路径方法的分词实现

这篇文章是我照着《基于N最短路径方法的中文词语粗分模型》这篇论文，自己用Python实现了下文中的算法，用于理解原理。

大致思想

考虑到汉语自动分词中存在切分歧义消除和未登录词识别两个主要问题，因此，有专家将分词过程分成两个阶段：首先采用切分算法对句子词语进行初步切分，得到一个相对最好的粗分结果，然后，再进行歧义排除和未登录词识别。
N-最短路径方法就是一种词语粗分模型，大致步骤：

• 1.根据词典，找出字串中所有可能的词，构造词语切分有向无环图。
• 2.每个词对应图中的一条有向边，并赋给相应的边长（权值） 。
• 3.然后针对该切分图，在起点到终点的所有路径中，求出长度值按严格升序排列（任何两个不同位置上的值一定不等）依次为第1、第2、…、第i、…、第N（N≥1）的路径集合作为相应的粗分结果集。
• 4.如果两条或两条以上路径长度相等，那么它们的长度并列第i，都要列入粗分结果集，而且不影响其他路径的排列序号，最后的粗分结果集合大小大于或等于N。

具体介绍

假设待分字符串$S=c_1c_2…c_n$，$c_i$是单个汉字，$n$是字符串的长度。

建立一个结点个数是$n+1$的有向无环图$G$，结点编号是$V_0,…V_n$。

通过以下的步骤建立可能的词边：

• 1.相邻结点$V_{k-1}， V_k;(1≤k≤n)$ 之间建立有向边$V_{k-1}$，$V_k$，边的长度值为$L_k$，边对应的词默认为$c_k(k＝1,2, …,n)$。
• 2.如果$w＝c_ic_{i＋1}…c_j;(0＜i＜j≤n)$是词表中的词，则结点$V_{i-1}，V_j$之间建立有向边$V_{i-1}, V_j$， 边的长度值为$L_w$， 边对应的词为$w$。

具体权重$L_k$和$L_w$的计算也有很多种方法，最简单的一种就是所有的权重都是1。

基于Dijkstra的贪心算法：

• 每个结点处记录$N$个最短路径值，并记录相应路径上当前结点的前驱。
• 如果同一长度对应多条路径，必须同时记录这些路径上当前结点的前驱，最后通过回溯即可求出NSP（NSP为结点$V_0$到$V_n$的前$N$个最短路径的集合）。

一个实例：句子：“他说的确实在理”

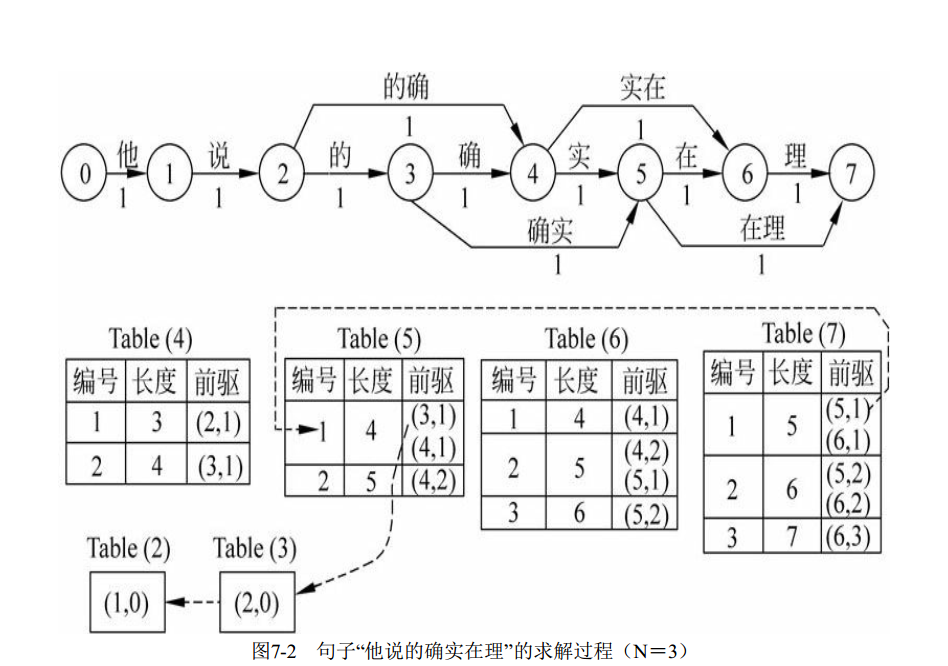
上面图中，$Table(i)$表示结点$i$的信息记录表，表里记录的是不同长度的路径的编号（不超过$N$），且从小到大排列。

前驱字段里的$(i,j)$表示沿当前路径到达当前结点的最后一条边的出发结点是$i$，这条边对应的是结点$i$的信息记录表中编号为$j$的路径。如果$j＝0$，表示没有其他候选的路径。

如结点$7$对应的信息记录表$Table(7)$中编号为1的路径前驱$(5,1)$表示前一条边为结点$5$的信息表中第$1$条路径。
信息记录表为系统回溯找出所有可选路径提供了依据。

实现

def get_dict(filename='SogouLabDic.dic.utf8'):
    """读取字典"""
    d = {}
    d['_t_'] = 0.0
    with open(filename, "r") as f:
        for line in f:
            word, freq = line.split('\t')[:2]
            d['_t_'] += int(freq)+1
            d[word] = int(freq)+1
    return d
d = get_dict()

# 为了使得演示效果和上面的图一致，去掉字典中原有的“他说”，加入没有的“在理”。

del(d["他说"])
d["在理"] = 1

def build_graph(s, big_dict):
    l = len(s)
    # 邻接矩阵，用dict实现
    adj = {}
    for i in range(l+1):
        adj[i] = {}
    for i in range(l):
        adj[i][i+1] = 1
    for size in range(2, l+1):
        for start in range(l+1):
            if start + size <= l and s[start: start+size] in big_dict:
                # 所有权值（长度）都直接选用1
                adj[start][start+size] = 1
    return adj

test_s = "他说的确实在理"
adj = build_graph(test_s, d)
print("邻接矩阵：", adj)

邻接矩阵： {0: {1: 1}, 1: {2: 1}, 2: {3: 1, 4: 1}, 3: {4: 1, 5: 1}, 4: {5: 1, 6: 1}, 5: {6: 1, 7: 1}, 6: {7: 1}, 7: {}}

邻接矩阵和上面的图可以一一对应。

def row_equal(row_1, row_2):
    """判断信息记录表中某两行是否重复"""
#     print(row_1, row_2)
    return row_1[1] == row_2[1] and row_1[2][0] == row_2[2][0] and row_1[2][1] == row_2[2][1]

def keep_n_min(candidates, n, length_index=1):
    """保留前N小的所有路径"""
    candidates = sorted(candidates, key=lambda x: x[length_index])
    last_one = -1
    count = 0
    last = -1
    for i, one in enumerate(candidates):
        if one[length_index] != last_one:
            last_one = one[length_index]
            count += 1
            if count > n:
                last = i
                break
    if last != -1:
        candidates = candidates[:last]
    index = 0
    # 更新路径编号
    last_len = -1
    del_indices = []
    for i, row in enumerate(candidates):
        if i > 0 and row_equal(candidates[i], candidates[i-1]):
            del_indices.append(i)
        if row[length_index] != last_len:
            last_len = row[length_index]
            index += 1
        candidates[i][0] = index
    for i in del_indices[::-1]:
        del candidates[i]
    return candidates

def get_tables_by_adj(adj, n):
    """使用类似Dijkstra的贪心算法获得信息表"""
    l = len(adj)
    tables = [[[1, 0, (0, 0)]]]  # 第0个table实际上用不到，这里初始化用于占位
    for cur in range(1, l):
        candidates = []
        i = 0
        for pre in range(cur):
            if cur in adj[pre]:  # 存在从结点pre指向结点cur的边
                for row in tables[pre]:
                    candidates.append([i, row[1] + 1, (pre, row[0])])
        # 保留长度前N小的所有candidate到table
        table = keep_n_min(candidates, n)
        tables.append(table)
    return tables

tables = get_tables_by_adj(adj, 3)
print("Table(i): 编号，长度，（前驱结点，前驱路径下标）")
for i, table in enumerate(tables):
    print("Table({}): ".format(i), table)

Table(i): 编号，长度，（前驱结点，前驱路径下标）
Table(0):  [[1, 0, (0, 0)]]
Table(1):  [[1, 1, (0, 1)]]
Table(2):  [[1, 2, (1, 1)]]
Table(3):  [[1, 3, (2, 1)]]
Table(4):  [[1, 3, (2, 1)], [2, 4, (3, 1)]]
Table(5):  [[1, 4, (3, 1)], [1, 4, (4, 1)], [2, 5, (4, 2)]]
Table(6):  [[1, 4, (4, 1)], [2, 5, (4, 2)], [2, 5, (5, 1)], [3, 6, (5, 2)]]
Table(7):  [[1, 5, (5, 1)], [1, 5, (6, 1)], [2, 6, (5, 2)], [2, 6, (6, 2)], [3, 7, (6, 3)]]

产生的信息记录表和上面图片中的一致，区别是，我不再使用只有一种情况的时候使用$j=0$的约定，即便是一种情况，也是$j=1$。
下面根据这些信息记录表回溯分词结果。

def core_retro(s, cur, pre, path_index, one_res, one_length_res, pre_node_index):
    """回溯的核心函数"""
    one_res.append(s[pre: cur]) 
    if pre == 0:
        one_length_res.append(one_res[::-1])
    else:
        for one_row in tables[pre]:
            if one_row[0] == path_index:
                core_retro(s, pre, one_row[pre_node_index][0], 
                           one_row[pre_node_index][1], one_res, one_length_res, pre_node_index)
                one_res.pop()

def retro_back(s, tables, n, length_index=1, pre_node_index=2):
    """根据信息记录表回溯分词结果"""
    count = 0
    last_len = -1
    res = {}
    l = len(s)
    for row in tables[-1]:
        # 只留长度是前n个的结果
        cur = l
        if row[length_index] != last_len:
            last_len = row[length_index]
            count += 1
            if count > n:
                break
        # 开始回溯
        one_length_res = []
        one_res = []
        # 回溯的核心函数
        core_retro(s, cur, row[pre_node_index][0], row[pre_node_index][1], one_res, one_length_res, pre_node_index)   
        if row[length_index] not in res:
            res[row[length_index]] = one_length_res
        else:
            res[row[length_index]] += one_length_res
    return res

res = retro_back(test_s, tables, 3)
res

{5: [['他', '说', '的', '确实', '在理'],
  ['他', '说', '的确', '实', '在理'],
  ['他', '说', '的确', '实在', '理']],
 6: [['他', '说', '的', '确', '实', '在理'],
  ['他', '说', '的', '确', '实在', '理'],
  ['他', '说', '的', '确实', '在', '理'],
  ['他', '说', '的确', '实', '在', '理']],
 7: [['他', '说', '的', '确', '实', '在', '理']]}

当$N=3$时，返回了3种长度的分词，7个分词结果。

参考资料：

• 《基于N最短路径方法的中文词语粗分模型》，张华平，刘群。
• 《自然语言处理》，宗庆成，第七章。