强化学习导论学习笔记——（七）

7. n-step Bootstrapping

n-step Bootstrapping简介

• 是MC方法和一步TD方法的结合。
• 是资格痕迹（eligibility traces，具体见第12章）的基础先验知识。

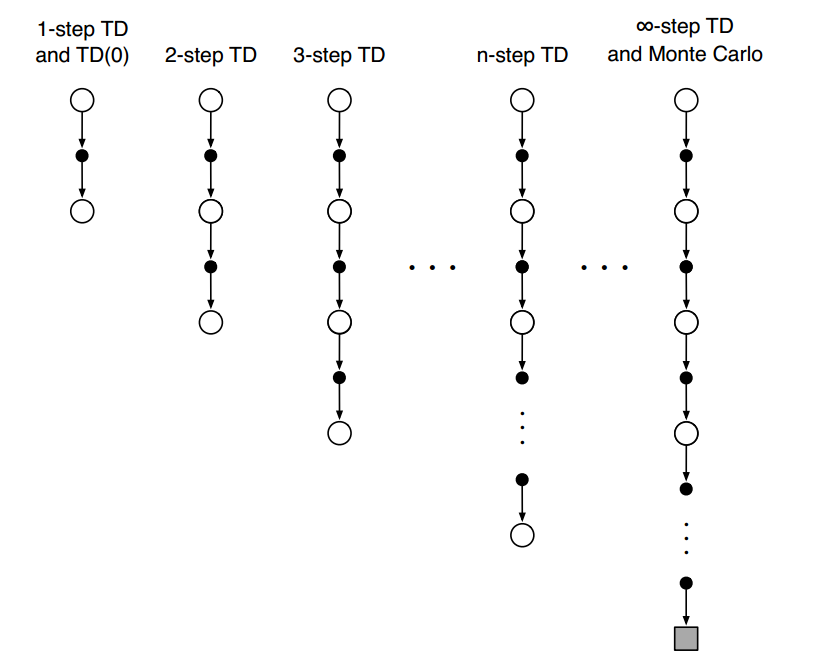
n-step TD Prediction

• MC对应的回报：$G_t = R_{t+1}+\gamma R_{t+2}+…+\gamma^{T-t-1}R_T$
• 一步TD对应的回报：$G_{t:t+1} = R_{t+1} + \gamma V_t(S_{t+1})$
• n-step的回报：$G_{t:t+n} = R_{t+1} + \gamma R_{t+2}+…+\gamma^{n-1}R_{t+n}+\gamma^nV_{t+n+1}(S_{t+n})$

核心代码：

def temporal_difference(value, n, alpha):
    ...
    
    # track the time
    time = 0

    # the length of this episode
    T = float('inf')
    while True:
        # go to next time step
        time += 1

        if time < T:
            # choose an action randomly
            if np.random.binomial(1, 0.5) == 1:
                next_state = state + 1
            else:
                next_state = state - 1

            if next_state == 0:
                reward = -1
            elif next_state == 20:
                reward = 1
            else:
                reward = 0

            # store new state and new reward
            states.append(next_state)
            rewards.append(reward)

            if next_state in END_STATES:
                T = time

        # get the time of the state to update
        update_time = time - n
        if update_time >= 0:
            returns = 0.0
            # calculate corresponding rewards
            for t in range(update_time + 1, min(T, update_time + n) + 1):
                returns += pow(GAMMA, t - update_time - 1) * rewards[t]
            # add state value to the return
            if update_time + n <= T:
                returns += pow(GAMMA, n) * value[states[(update_time + n)]]
            state_to_update = states[update_time]
            # update the state value
            if not state_to_update in END_STATES:
                value[state_to_update] += alpha * (returns - value[state_to_update])
        if update_time == T - 1:
            break
        state = next_state

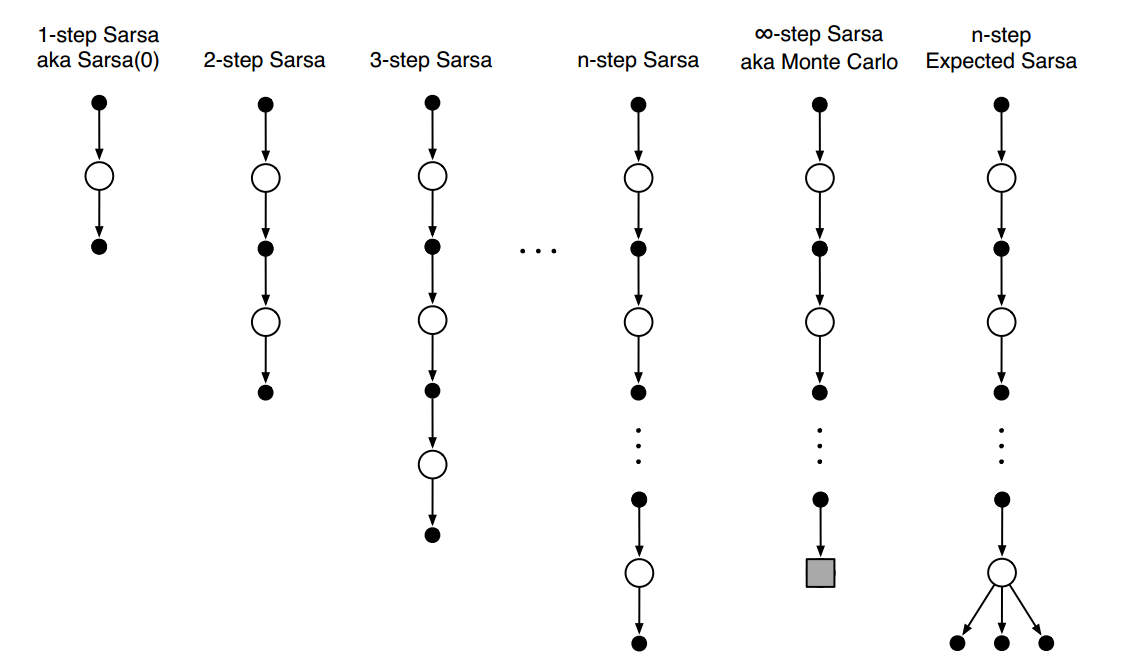
n-step Sarsa

• n-step Sarsa:
• 回报：$G_{t:t+n} = R_{t+1} + \gamma R_{t+2} + \gamma^{n-1} R_{t+n} + \gamma^nQ_{t+n-1}(S_{t+n}, A_{t+n})$
• 更新动作价值函数：$Q_{t+n}(S_t, A_t) = Q_{t+n-1}(S_t, A_t) + \alpha[G_{t:t+n} - Q_{t+n-1}(S_t,A_t)]$
• n-step Expected Sarsa:
• 回报：$G_{t:t+n} = R_{t+1} + \gamma R_{t+2} + \gamma^{n-1} R_{t+n} + \gamma^n \bar V_{t+n-1}(S_{t+n})$
• 更新价值函数：$\bar V_t(s) = \sum_a \pi(a|s)Q_t(s,a)$

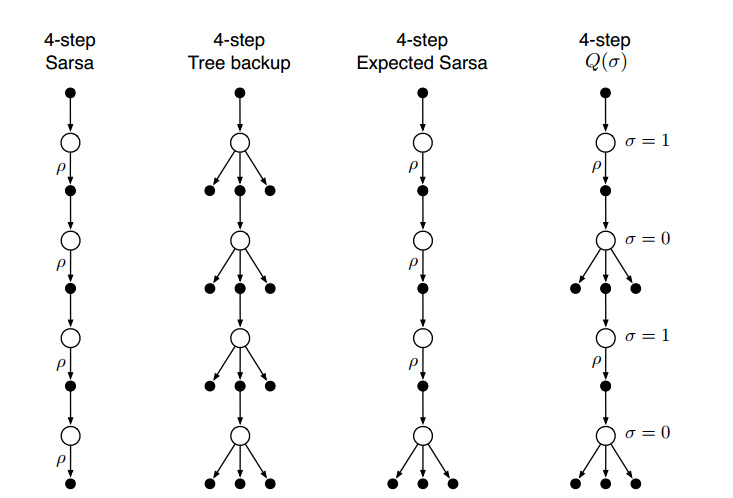
n-step off-policy with Importance Sampling

更新动作价值函数：

$$Q_{t+n}(S_t， A_t) = Q_{t+n-1}(S_t, A_t) + \alpha \rho_{t:t+n-1}[G_{t:t+n} - Q_{t+n-1}(S_t, A_t)]$$

其中，重要性采样比例：

$$\rho_{t:h} = \prod_{k=t}^{min(h,T-1)}\frac{\pi(A_k|S_k)}{b(A_k, S_k)}$$

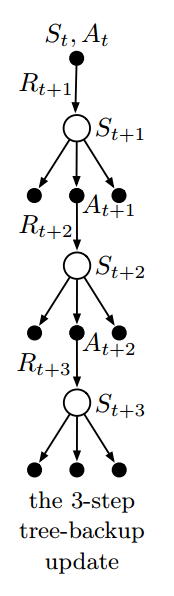
n-step Tree Backup Algorithm

不需要重要性采样。

使用所有叶子节点的动作价值函数去更新动作价值函数。

回报：

$$G_{t:t+n} = R_{t+1} + \gamma \sum_{a\neq A_{t+1}}\pi(a|S_{t+1})Q_{t+n-1}(S_{t+1}, a) + \gamma\pi(A_{t+1}|S_{t+1})G_{t+1:t+n}$$

n-step $Q(\sigma)$

$\sigma$代表是否使用全采样。

回报：

$$G_{t:h} = R_{t+1} + \gamma(\sigma_{t+1}\rho_{t+1}+(1-\sigma_{t+1})\pi(A_{t+1}|S_{t+1}))(G_{t+1:h}-Q_{h-1}(S_{t+1}, A_{t+1})) + \gamma \bar V_{h-1}(S_{t+1})$$