遗传算法（Genetic Algorithm）

Posted on | In | Visitors:

这篇博客记录自己学习遗传算法的心得。

引入

关于遗传算法，在知乎的问题如何通俗易懂地解释遗传算法？有什么例子？是一个很好的资料，介绍了很多很有趣的例子。

我第一次对遗传算法感兴趣是听了卓老板的一个介绍复杂系统的音频节目，这个节目引用了《复杂》这本书中的关于遗传算法的例子。即一个吃豆人的例子，知乎也有提到。很有意思，也很有启发性，于是想研究研究代码，顺带做个总结。

来自遗传学的启发

看看遗传算法用到了哪些来自遗传学的启发：

  1. 达尔文的“自然选择”：即优胜劣汰，适应环境的个体可以繁衍后代，而不适应环境的个体不能繁衍后代；
  2. “交叉”：子代的基因一半来自父亲，一半来自母亲；
  3. “基因突变”：子代的基因在继承父母的基因的基础上会有一定的概率发生突变。

遗传算法介绍

遗传算法的输入包括两个部分：

候选程序群体和适应性函数

  • 候选程序群体 也就是“基因”，这个概念需要好好理解。它可以表示成位/数字或符号组成的字符串。一般来说，它代表“环境状态”–>“反应动作”的映射，也就是代表不同的情况下，它该做什么动作。这个概念还有很多玄机，后面继续谈。
  • 适应性函数 也就是“大自然”，可以理解成评价函数，评价某个个体对某个特定环境的适应程度，适应程度高的个体可以繁殖后代。

GA算法：

  1. 生成候选方案的初始群体。生成初始群体最简单的办法就是随机生成大量“个体”（个体基因）。
  2. 计算当前群体中各个个体的适应度。
  3. 选择一定数量适应度最高的个体作为下一代的父母。
  4. 将选出的父母进行配对。用父母进行重组产生出后代，伴有一定的随机突变概率，后代加入形成新一代群体。选出的父母不断产生后代，直到新的群体数量达到上限（即与初始群体数量一样）。新的群体成为当前群体。
  5. 转到第2步。

遗传算法的应用

  • 通用电气将GA用于飞行器的部分自动化设计；
  • 洛斯阿拉莫斯国家实验室用GA分析卫星图像；
  • 约翰迪尔（John Deere）公司将GA用于自动化生产线的调度；
  • 德州仪器（Texas Instruments）则用GA来设计计算机芯片。

举例

例子1：垃圾清扫机器人

例子采用《复杂》中的吃豆人，也就是易拉罐清扫机器人————罗比。

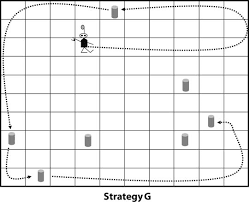
罗比是图中的机器人，它的任务，是打扫10×10方格中随机出现的易拉罐。

每次清扫工作，罗比可以执行200个动作。罗比只能看见当前的格子和相邻4个格子的情况。

每个格子只有3种情况：

  • 空格子
  • 有易拉罐的格子
  • 墙。

动作可以是以下7种：

  • 往北移动
  • 往南移动
  • 往东移动
  • 往西移动
  • 随机移动
  • 不动
  • 收集罐子。
  • 动作对应的奖励和惩罚：
  • 收集一个罐子，+10分；
  • 进行收集动作，但格子中没有罐子，-1分；
  • 撞到墙-5分，回到原来的格子。

显然，罗比尽可能地多收集罐子，别撞墙，没罐子的时候别去捡，得到的分数就最高。

直接写规则好吗？

人工智能早期的“符号学派”，设计一个智能系统通常是基于规则去判断的。

突然想到知乎上一个很搞的问题：如何看待百度无人车，三千多个场景，一万多个if？。

这些说白了，这些规则，就是我上文说的“环境状态”–>“反应动作”的映射。

回到罗比的问题，如果我们的罗比是一个没有“记忆”的机器人，也就是说，它只能应用的信息是当前所处格子和其他相邻的四个格子的状态，却不知道它上一步走的时候那5个格子的状态。

这样问题就会大大简化，场景的个数就变成了3的5次方（5个格子，每个格子可能有3中状态），也就是243种情况。

没有问题，这样写规则也能解决。但，这样实在是费时费力，这里还只考虑罗比没有记忆呢，如果罗比能记住前面走过的一步，那规则就是$243^2$条了，那已经没法写了，更别说记住前面两步，三步了。

好，既然这样，让罗比试试遗传算法：

  1. 生成初始群体。初始群体有200个随机个体（策略）。每个基因是一个介于0和6之间的数字，代表一次动作（0=向北移动，1=向南移动，2=向东移动，3=向西移动，4=不动，5=捡拾罐子，6=随机移动）。在初始群体中，基因都随机设定。程序中用一个伪随机数发生器来进行各种随机选择。重复后面的步骤1000次。
  2. 计算群体中每个个体的适应度。在我的程序中，是通过让罗比执行100次不同的清扫任务来确定策略的适应度。每次将罗比置于位置（0，0），随机撒一些易拉罐（每个格子至多1个易拉罐，格子有易拉罐的概率是50%）。然后让罗比根据策略在每次任务中执行200个动作。罗比的得分就是策略执行各任务的分数。策略的适应度是执行100次任务的平均得分，每次的罐子分布都不一样。
  3. 进化。让当前群体进化，产生出下一代群体。即重复以下步骤，直到新群体有200个个体。

作者自己编写的规则，平均得分是346，完美的得分是500（一共50个罐子），GA结果是483，相当不错。

讲到这里，还没有说遗传算法最神奇的一点：那就是，根据遗传算法得到的规则，单个拿出来看，可能人们很难理解。

这其实很好理解，拿基因来说吧，如果让你设计一个“完美”的人，你可能会想，“我要设计一个大眼睛的基因，我还要设计一个高鼻梁的基因”，但是局部可能都是比较不错的策略，综合在一起的结果，可能没那么好。也许真正看上去完美的人，眼睛不是最大，鼻梁也不是最高，但这个人整体看上去就是很好看。

难怪美国国家航空航天局（NASA）的遗传算法专家罗恩（Jason Lohn）曾这样说：“遗传算法是探索设计死角的伟大工具。”

例子2：求解函数

求解函数$f(x) = x + 10×sin(5×x) + 7*cos(4×x)$ 在区间[0,9]的最大值。（来自知乎）

如何应用遗传算法求解这样的最优化问题呢？

还是先解决GA算法的两个输入：

  • 候选程序群体是什么？适应性函数是什么？
  • 适应性函数：比较容易想到，本身就是求解最大值，函数本身就可以当做适应性函数。
  • 候选程序群体：题目给出了探索的解的空间，在0-9之间比如划分成90000，即精确到4位小数；

$2^{16}<90000<2^{17}$，需要17位二进制数来表示这些解。换句话说，一个解的编码就是一个17位的二进制串。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127

import math
import random
import operator

class GA():
    def __init__(self, length, count):
        # 染色体长度
        self.length = length
        # 种群中的染色体数量
        self.count = count
        # 随机生成初始种群
        self.population = self.gen_population(length, count)

    def evolve(self, retain_rate=0.2, random_select_rate=0.5, mutation_rate=0.01):
        """
        进化
        对当前一代种群依次进行选择、交叉并生成新一代种群，然后对新一代种群进行变异
        """
        parents = self.selection(retain_rate, random_select_rate)
        self.crossover(parents)
        self.mutation(mutation_rate)

    def gen_chromosome(self, length):
        """
        随机生成长度为length的染色体，每个基因的取值是0或1
        这里用一个bit表示一个基因
        """
        chromosome = 0
        for i in xrange(length):
            chromosome |= (1 << i) * random.randint(0, 1)
        return chromosome

    def gen_population(self, length, count):
        """
        获取初始种群（一个含有count个长度为length的染色体的列表）
        """
        return [self.gen_chromosome(length) for i in xrange(count)]

    def fitness(self, chromosome):
        """
        计算适应度，将染色体解码为0~9之间数字，代入函数计算
        因为是求最大值，所以数值越大，适应度越高
        """
        x = self.decode(chromosome)
        return x + 10*math.sin(5*x) + 7*math.cos(4*x)

    def selection(self, retain_rate, random_select_rate):
        """
        选择
        先对适应度从大到小排序，选出存活的染色体
        再进行随机选择，选出适应度虽然小，但是幸存下来的个体
        """
        # 对适应度从大到小进行排序
        graded = [(self.fitness(chromosome), chromosome) for chromosome in self.population]
        graded = [x[1] for x in sorted(graded, reverse=True)]
        # 选出适应性强的染色体
        retain_length = int(len(graded) * retain_rate)
        parents = graded[:retain_length]
        # 选出适应性不强，但是幸存的染色体
        for chromosome in graded[retain_length:]:
            if random.random() < random_select_rate:
                parents.append(chromosome)
        return parents

    def crossover(self, parents):
        """
        染色体的交叉、繁殖，生成新一代的种群
        """
        # 新出生的孩子，最终会被加入存活下来的父母之中，形成新一代的种群。
        children = []
        # 需要繁殖的孩子的量
        target_count = len(self.population) - len(parents)
        # 开始根据需要的量进行繁殖
        while len(children) < target_count:
            male = random.randint(0, len(parents)-1)
            female = random.randint(0, len(parents)-1)
            if male != female:
                # 随机选取交叉点
                cross_pos = random.randint(0, self.length)
                # 生成掩码，方便位操作
                mask = 0
                for i in xrange(cross_pos):
                    mask |= (1 << i) 
                male = parents[male]
                female = parents[female]
                # 孩子将获得父亲在交叉点前的基因和母亲在交叉点后（包括交叉点）的基因
                child = ((male & mask) | (female & ~mask)) & ((1 << self.length) - 1)
                children.append(child)
        # 经过繁殖后，孩子和父母的数量与原始种群数量相等，在这里可以更新种群。
        self.population = parents + children

    def mutation(self, rate):
        """
        变异
        对种群中的所有个体，随机改变某个个体中的某个基因
        """
        for i in xrange(len(self.population)):
            if random.random() < rate:
                j = random.randint(0, self.length-1)
                self.population[i] ^= 1 << j


    def decode(self, chromosome):
        """
        解码染色体，将二进制转化为属于[0, 9]的实数
        """
        return chromosome * 9.0 / (2**self.length-1)

    def result(self):
        """
        获得当前代的最优值，这里取的是函数取最大值时x的值。
        """
        graded = [(self.fitness(chromosome), chromosome) for chromosome in self.population]
        graded = [x[1] for x in sorted(graded, reverse=True)]
        return ga.decode(graded[0])     


if __name__ == '__main__':
    # 染色体长度为17， 种群数量为300
    ga = GA(17, 300)

    # 200次进化迭代
    for x in xrange(200):
         ga.evolve()

    print(ga.result())
1
7.85672650701

例子3：用n个三角形作画

GA画画，这些同学脑洞开得很大，很有趣～
上传一张图片，GA自己学习用三角形组合出原图。