EM算法总结
在概率模型中,最常用的模型参数估计方法应该就是最大似然法。
EM算法本质上也是最大似然,它是针对模型中存在隐变量的情况的最大似然。
下面通过两个例子引入。
没有隐变量的硬币模型
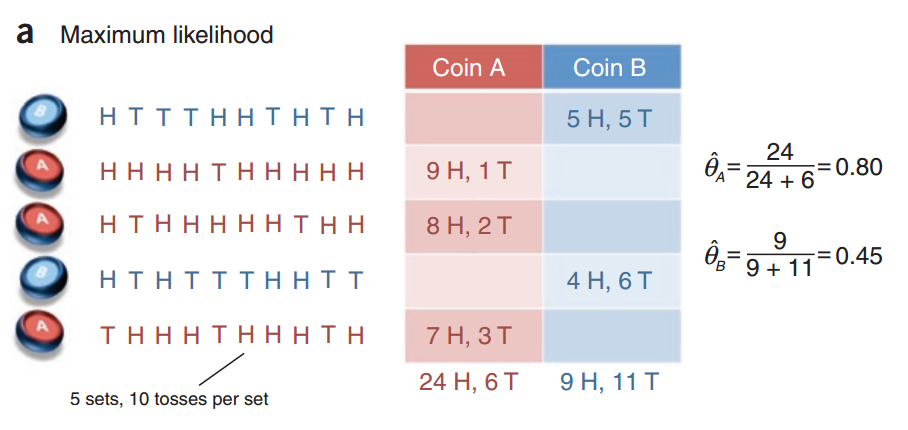
假设有两个硬币,$A$和$B$,这两个硬币具体材质未知,即抛硬币的结果是head的概率不一定是50%。
在这个实验中,我们每次拿其中一个硬币,抛10次,统计结果。
实验的目标是统计$A$和$B$的head朝上的概率,即估计$\hat \theta_A$和$\hat \theta_B$。
对每一枚硬币来说,使用极大似然法来估计它的参数:
假设硬币$A$正面朝上的次数是$n^A_h$,反面朝上的次数是:$n^A_t$。
似然函数:$L(\theta_A) =(\theta_A)^{n^A_h}(1-\theta_A)^{n^A_t}$。
对数似然函数:$log;L(\theta_A) = n^A_h\cdot log(\theta_A)+n^A_t\cdot log(1-\theta_A)$。
$\hat \theta_A = \underset{\theta_A}{argmax};log;L(\theta_A)$ 。
对参数求偏导:$\frac{\partial log; L(\theta_A)}{\partial \theta_A}=\frac{n^A_h}{\theta_A}-\frac{n^A_t}{1-\theta_A}$。
令上式为$0$,解得:$\hat \theta_A = \frac{n^A_h}{n^A_h+n^A_t}$。
即$\hat \theta_A = \frac{number\; of\; heads\; using\; coin\; A}{total\; number\; of\; flips\; using\; coin\; A}$。
有隐变量的硬币模型
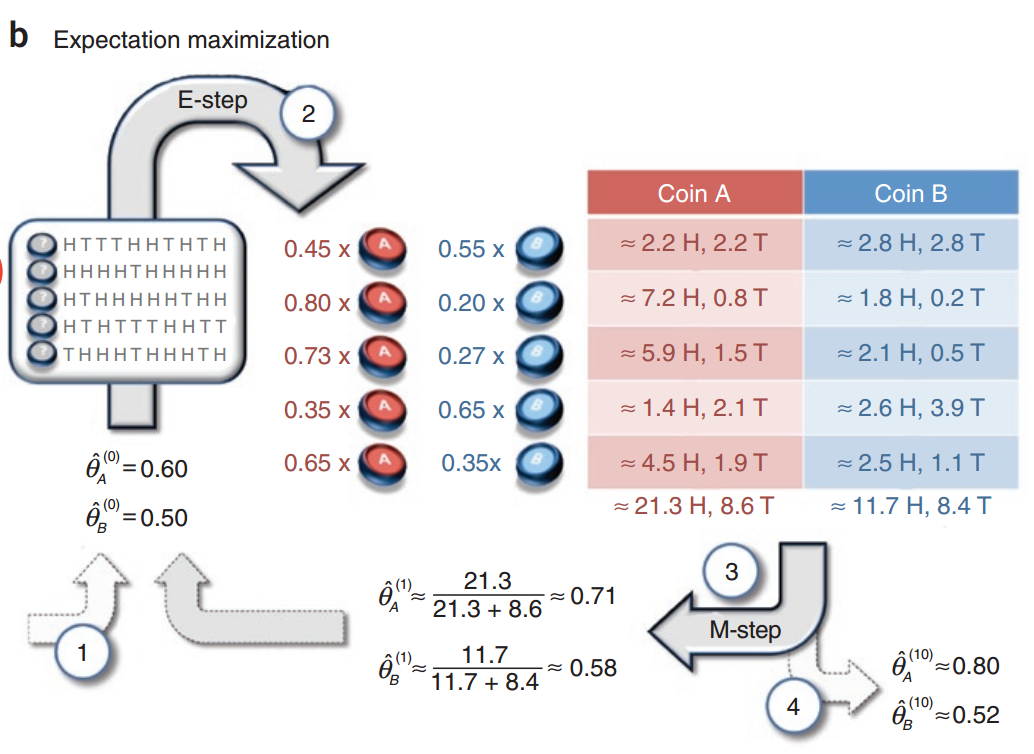
这个问题是上一个问题的困难版,即给出一系列统计的实验,但不告诉你某组实验采用的是哪枚硬币,即某组实验采用哪枚硬币成了一个隐变量。
这里引入EM算法的思路:
- 1.先随机给出模型参数的估计,以初始化模型参数。
- 2.根据之前模型参数的估计,和观测数据,计算隐变量的分布。
- 3.根据隐变量的分布,求联合分布的对数关于隐变量分布的期望。
- 4.重新估计模型参数,这次最大化的不是似然函数,而是第3步求的期望。
一般教科书会把EM算法分成两步:E步和M步,即求期望和最大化期望。
E步对应上面2,3;M对应4。
EM算法
输入:观测变量数据$Y$,隐变量数据$Z$,联合分布$P(Y,Z|\theta)$,条件分布$P(Z|Y,\theta)$;
输出:模型参数$\theta$。
- 1.选择参数的初始值$\theta^{(0)}$,开始迭代;
- 在第$i+1$次迭代:
- 2.E步:$Q(\theta,\theta^{(i)}) = \sum_zlog;P(Y,Z|\theta)P(Z|Y,\theta^{(i)})$
- 3.M步:$Q^{(i+1)} = \underset{\theta}{argmax};Q(\theta,\theta^{(i)})$
- 4.重复2,3直至收敛。