如何优雅地手推SVM
1.手推失败原因总结
- 没有重点。完整的推倒过程非常复杂,全部讲清楚是一个大工程,如何选择重点非常重要,如果只是花时间去记具体细节的公式化简,很容易手推失败。
- 先验知识掌握不牢。 比如KKT/Hinge Loss/kernel。 这些知识应该拆开来分块学,避免学混了,以为kernel就是给SVM用的。
- 在模型中使用trick的地方没有着重记忆。
2.先验知识
2.1 拉格朗日对偶性
原始问题:
$f(x),c_i(x),h_j(x)$是定义在$R^n$上的连续可微函数,考虑约束最优化问题:
$$\underset{x\in R^n}{min}f(x)$$
$$s.t. \; c_i(x)\leq 0 \;\; i=1,…,k$$
$$h_j(x)=0 \;\; j=1,…,l$$
即有$k$个不等式约束:$c_i(x)$和$l$个等式约束:$h_j(x)$。
拉格朗日函数:
- $L(x,\alpha,\beta)=f(x)+\sum_{i=1}^k\alpha_i c_i(x)+\sum_{j=1}^l\beta_jh_j(x)$
- $\alpha_i$和$\beta_j$,称为拉格朗日乘子,$\alpha_i\geq 0$。
拉格朗日函数的极大极小问题:
- 令$\theta_P(x) = \underset{\alpha,\beta}{max};L(x,\alpha,\beta)$
- 如果存在$x$违反了原始问题的约束条件,则$\theta_P(x)=\infty$,当$x$不违反原始问题的约束条件,则$\theta_P(x)=f(x)$
- 因此:$\underset{x}{min}\theta_P(x)=\underset{x}{min}\underset{\alpha,\beta}{max}L(x,\alpha,\beta)$等价于原问题。
对偶问题:
- $\underset{\alpha,\beta}{max}\underset{x}{min};L(x,\alpha,\beta)$
- 定理:如果函数$f(x)$和$c_i(x)$是凸函数,$h_j(x)$是仿射函数,则$x^*,\alpha^*,\beta^*$是同时是原始问题和对偶问题的解的必要条件是满足KKT条件。
KKT条件:
- 1.拉格朗日函数对$x$,$λ$,$α$求偏导都为0:
- $\triangledown_xL(x^*,\alpha^*,\beta^*)=0$
- $\triangledown_{\alpha}L(x^*,\alpha^*,\beta^*)=0$
- $\triangledown_{\beta}L(x^*,\alpha^*,\beta^*)=0$
- 2.对于不等式约束,$\alpha_i^*c_i(x^*)=0\;\;\;i=1,…,k$(对偶互补条件)。
2.2 Hinge Loss
对于二分类问题:
$HingeLoss = max(0, 1-y_{true}\cdot y_{pred})$,也就是说,如果$y_{true}\cdot y_{pred}>1$,$HingeLoss=0$,在svm中,$y_{true}\cdot y_{pred}=y_{true}(w\cdot x+b)$,即函数间隔。也就是说,我们希望这个函数间隔大于1就好,具体在svm上的应用,后文继续。

对于ranking问题:
$HingeLoss(f) = max(0, 1-f(a)+f(a’))$,下面介绍下ranking的$HingeLoss$的intuition。
三元组:$(r,a,a’)$代表rater(评分人),$a$和$a’$代表两个app,并且$a$的评分高于$a’$。我们需要找到一个ranking方式,使得对所有$a > a’$,都有$f(a) > f(a’)$。
最直接地,会想到0-1损失函数,即$mistake_j(f) = 1, \; if\; f(a) < f(a’) + 1$,$mistake_j(f) = 0, \;if\; f(a) >= f(a’) + 1$,然后最终的损失函数是:$M = \sum_j mistake_j(f)$。
但是这么做,M是非凸的,直接使用梯度下降去优化很可能只能获得局部最优。
所以使用$hinge_j(f) = max(0, 1-f(a)+f(a’))$来替换$mistake_j(f)$,这样最终的损失函数是凸函数。
2.3 Kernel Trick
简单地说,Kernel Trick通过一个非线性变换,将输入空间(欧氏空间$R^n$或者离散集合)映射到特征空间(希尔伯特空间$Η$),一般是升维的映射,所以有些人会说核技巧就是升维的,但这个说法并不严谨。
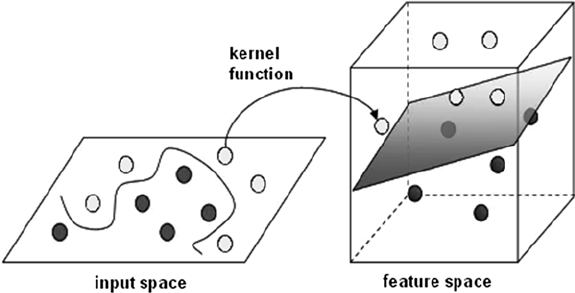
核函数:
设$X$是输入空间(欧氏空间$R^n$或者离散集合),$H$是特征空间(希尔伯特空间),若存在一个从$X$到$H$的映射,即$φ(x):X\rightarrow H$,使得对所有$x,z∈X$,有$K(x,z)=φ(x)\cdot φ(z)$,也就是说核函数是两个映射函数的点乘。
核技巧:
核技巧不显式地定义映射函数$φ(x)$,只定义$K(x,z)$,这样计算更容易。
常用的核函数:
- 多项式核函数(polynomial kernel function):$K(x,z) = (x\cdot z)^p$
- 高斯核函数(Gaussian kernel function):$K(x,z) = exp(-\frac{||x-z||^2}{2σ^2})$
3 具体推导
3.1 硬间隔最大化
对于二分类线性可分的问题,我们想要找到一个分割超平面,使得在平面的正面一侧的点都是正类,在反面一侧的点都是负类。
分割超平面的表达式:$wx+b=0$。
svm的独特之处在于,它认为什么样的分割超平面是最好的,也就是分割超平面的评价标准。这个评价标准就是:两边离超平面最近的点,它们离超平面的距离要最远。用通俗一点的话去类比就是,如果要评价一个酒店的服务质量好坏,可以比较它们的差评,哪个差评相对好一些的,就认为这个酒店服务质量还不错。两边离分割超平面最近的点即支撑向量(support vector)。
假设我们找到了这些点,并做两个平行于分割超平面的支撑平面。
两个支撑平面的表达式:
$wx+b=1$,$wx+b=-1$;

上面的支撑平面使用了第一个trick,也就是限定支撑平面等式右面的系数是$1$和$-1$,这是利用了$w$和$b$可以等比例缩放的性质,固定支撑平面的系数,可以方便后续计算。
对于所有训练数据:
要满足$wx_++b≥1$,$wx_-+b≤-1$;
因为$y_+=1$,$y_-=-1$,可以使用使用一个trick将上面两个式子合成一个:
$y(wx+b)≥1$
下面是个重点,来推导两个支撑平面的间隔:
$width=(x_+-x_-)\frac{w}{||w||}=\frac{x_+w}{||w||}-\frac{x_-w}{||w||}=\frac{2}{||w||}$
而最大化$\frac{2}{||w||}$和最小化$\frac{1}{2}||w||^2$是等价的,至此问题转换成了一个带不等式约束的凸优化问题,其中的不等式约束是:$y(wx+b)≥1$。
参考上面介绍的KKT条件,拉格朗日函数为:$L(w,b,α)=\frac{1}{2}||w||^2-\sum_1^Nα_iy_i(wx_i+b)+\sum_1^Nα_i$,问题转换为:$\underset{w,b}{min};\underset{α,α\geq 0}{max}L(w,b,α)$。令拉格朗日函数对$w$和$b$求偏导,并使之为0,可以得到:$w=\sum_i^Nα_iy_ix_i$,$\sum_i^Nα_iy_i=0$。
从$w=\sum_i^Nα_iy_ix_i$可以看出,模型的参数$w$可以完全用数据和$α$来计算,模型在优化的时候,**保存的参数是$α$**。优化完$α$以后,直接计算出$w$即可。
继续回到推导上来,将上面的两个式子带回到拉格朗日函数,化简得到:$L(w,b,α)=-\frac{1}{2}\sum_i^N\sum_j^Nα_iα_jy_iy_j(x_i\cdot x_j)+\sum_i^Nα_i$。
问题通过引入KKT条件做了一番推导以后可以归纳成:
$minL(α) = \frac{1}{2}\sum_i^N\sum_j^Nα_iα_jy_iy_j(x_i\cdot x_j)-\sum_i^Nα_i$
约束条件:$\sum_i^Nα_iy_i=0$和$α_i\geq 0$。
推导到这里,可以直接把问题交给优化算法SMO了。SMO算法就不展开说了,这篇文章不错,可以参考。
3.2 软间隔最大化
硬间隔最大化的一个很难实现的前提是:线性可分。现实中很多数据正负类相互交缠,不太可能严格满足线性可分,这个时候就需要软间隔最大化。
可以认为存在一些特异点(outlier),去除了这些特异点之后,模型依然是可分的。
于是引入一个**松弛变量$ξ_i$**,约束条件变成:$y_i(wx_i+b)≥1-ξ_i$。
再引入惩罚参数:$C>0$,目标函数变成:$min;\frac{1}{2}||w||^2+C\sum_i^Nξ_i$。
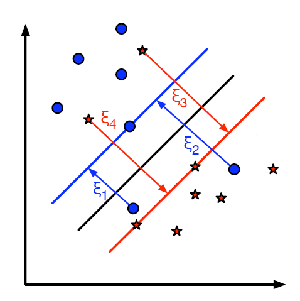
接下来的推导和硬间隔的类似,最终的优化式子不变,只有其中一个约束变成:$0 \leq α_i\leq C$
得出了这个结果之后,我们终于到了Hinge Loss了,让我们来看看软间隔最大化和Hinge Loss的关系:
软间隔最大化:
目标函数:
$\underset{w,b,ξ}{min}\frac{1}{2}||w||^2+C\sum_i^Nξ_i$
约束条件:
$y_i(wx_i+b)≥1-ξ_i$,$ξ_i \geq 0$
Hinge Loss:
目标函数:
$min \sum_i^N max(0, 1-y_i(wx_i+b)) + λ||w||^2$
证明等价:从Hinge Loss往回推导,令$1-y_i(wx_i+b)=ξ_i$,且$ξ_i \geq 0$,于是有$max(0, 1-y_i(wx_i+b))=max(0,ξ_i)=ξ_i$,所以Hinge Loss变成了$\underset{w,b}{min}; \sum_i^Nξ_i + λ||w||^2$。取$λ=\frac{1}{2C}$,又写成:$\frac{1}{C}(C\sum_i^Nξ_i + \frac{1}{2}||w||^2)$,与软间隔最大化等价。
非线性支持向量机
从推导后的式子可以看出,目标函数只使用了数据集两两点乘的结果。这样我们可以直接使用核函数来代替这个点乘,实现空间非线性映射。
非线性支持向量机表述:
目标函数:
$minL(α) = \frac{1}{2}\sum_i^N\sum_j^Nα_iα_jy_iy_jK(x_i,x_j)-\sum_i^Nα_i$
约束条件:$\sum_i^Nα_iy_i=0$和$0 \leq α_i \leq C$。
分割平面:
$\sum_i^Nα_iy_iK(x,x_i)+b$