Javen Chen's Blog

1.手推失败原因总结

1. 没有重点。完整的推倒过程非常复杂，全部讲清楚是一个大工程，如何选择重点非常重要，如果只是花时间去记具体细节的公式化简，很容易手推失败。
2. 先验知识掌握不牢。 比如KKT/Hinge Loss/kernel。 这些知识应该拆开来分块学，避免学混了，以为kernel就是给SVM用的。
3. 在模型中使用trick的地方没有着重记忆。

2.先验知识

2.1 拉格朗日对偶性

原始问题：

是什么

提到**Principal component analysis (PCA)**，大家会先想到“降维”，其准确的定义是：

1

PCA is a statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables called principal components.

翻译：

PCA是一种统计过程，它使用正交变换，将一系列可能相关的变量的观测转换到另外一系列的线性无关的变量，这些线性无关的变量称为主成分。

动机

首先，来说说为什么要写LR和ME。最近在研究《 An Introduction to Conditional Random Fields for Relational Learning》，发现了一张神图。

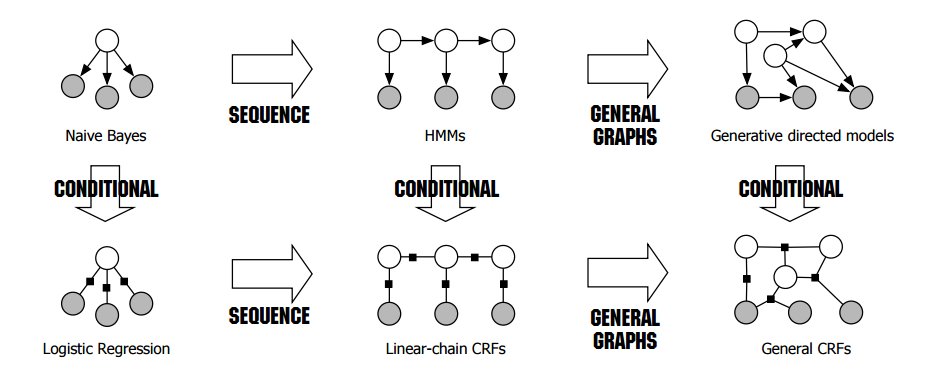
稍微解释一下：我们把机器学习模型分为两类，一类是生成模型，一类是判别模型。第一行的都是生成模型，第二行的都是判别模型。所谓生成模型是通过建模$P(x,y)$，判别模型是直接建模$P(y|x)$。把这两种建模思维和图模型相结合，我们可以描述随机变量之间的关系，使得模型变得复杂。一般这些随机变量是同一类型的在不同时间序列上的变量，具体关系由图模型描述。

从图上看，关系最简单的，是朴素贝叶斯模型和LR(ME)模型。这里把LR和ME归为了一类，这是因为LR和ME在本质上是等价的（虽然他们的建模思想完全不同），都是属于对数线性模型，也都是判别模型。朴素贝叶斯很简单了，就不多说了，LR和ME却还可以引申出很多知识点，比如拉格朗日对偶，最优化方法。这些都在后面的博文中详细描述。这里专注把LR和ME的思路理清，以及它们背后的intuition。最后使用Theano实现。

机器学习中的Monte-Carlo

来说一下机器学习中Monte-Carlo中用在什么地方：

• 贝叶斯推论和学习：
  • 归一化：$p(x | y) =\frac{p(y | x)p(x)}{\int_Xp(y| x’)p(x’)dx’}$
  • 边缘概率的计算：$p(x | y) = \int_Z p(x, z | y)dz$
  • 求期望：$E_{p(x|y)}(f(x)) = \int_Xf(x)p(x|y)dx$
• 上面三处都用到了积分，Monte-Carlo的核心思想即用样本的和去近似积分。

随机采样介绍

所谓采样，实际上是指根据某种分布去生成一些数据点，比如“石头剪刀布”的游戏，服从均匀分布，且概率都是三分之一，采样即希望随机获得一个“石头”或者“剪刀”或者“布”，并且每中情况出现的机会应该是一样的。也就是说，这是我们根据观察数据再确定分布的过程的逆过程。

Back Propagation （BP）

the code is from here.
Here is his
blog.

1. The four fundamental equations behind backpropagation definition:

$$δ^l_j=\frac{∂C}{∂a^l_j}$$

==>

1. 介绍和引入

最近初学NLP相关的深度学习，下了很多论文，数量一多，发现论文管理是个问题。

首先论文数目一多，必须要按类别放到子文件夹下。但是某一篇论文，往往有多个主题。比如说某论文使用word2vec给短文本分类，那这篇论文既可以放在word2vec的目录下，也可以放在短文本的目录下，也可以放在分类的目录下。当你有天想去看了，往往又忘了是放在哪个子目录下了。再比如说，你下载了一些论文，下载的时候你知道这些论文的重要性（引用次数或者对项目的重要性）和紧急性（比如你三天之内都要看完）。但是当你把它放在某个子目录以后，当你有时间去看的时候，你忘了你当时最想看的那篇论文是什么了。

为此，我决定开发一个小工具来帮助我管理我的paper。我的思路是这样的：给每篇论文打上tag，标上重要程度和紧急程度。这样当我没有特定目的的时候，我就可以根据重要程度和紧急程度看小工具推荐的paper；当我想看某方面的paper时，我只需要查询下tag就可以找到相关主题的paper。

OK，有了思路，就可以着手实现了。

概述

1
2
3

自然语言分类是指按照预先定义的主题类别，为文档集合中的每个文档确定一个类别。
本文将介绍一个限定类别的自然语言分类器的原理和实现。采用Python作为编程语言，采用朴素贝叶斯作为分类器，使用jieba进行分词，并使用scikit-learn实现分类器。
训练数据来自于凤凰网，最终交叉验证的平均准确率是0.927。

一、训练数据获取

中文自然语言分类现成可用的有搜狗自然语言分类语料库、北京大学建立的人民日报语料库、清华大学建立的现代汉语语料库等。

由于语言在使用过程中会不断演进，具有一定的时效性，我们最终决定自己开发爬虫爬取训练数据。

这两天也不算忙，可是总是没有找到时间像这样地静下心来感觉一下。晚上寝室只有我一个人，是个好时机去记录前些天的想法。

前些日子又重新读了一遍《挪威的森林》，动机像是想念一个老友，或者应该说是想念去年这个时候看这本书的感觉。但去年的感觉，仅仅是感觉，这回可以用文字稍稍记录。说实话第一天晚上打开书的时候就感觉到一股沉闷的压抑。那口井，深不见底的黝黑的井，以及美丽而脆弱地像玻璃的直子，以及迷茫不知所措的渡边，这些东西唤起了一些实在难称得上是愉悦的共鸣。后来我看得实在头疼，于是出去透了透气，喝了杯饮料，感觉才好些。

我现在感觉村上有些自闭，虽然他一直声称自己在不停地寻求沟通与理解。但他的思想，仿佛仅仅只是属于他一个人的，外界东西很不容易进来，他一直在阅读，思考，但却也一直沉默，像一个修行者。但这却也难免。今天看了林少华写的余秋雨与村上笔下的欧洲的区别，说到底，余秋雨与村上的区别就是村上比余秋雨更具有人性的关怀，而这种关怀，是基于对人性的丑恶的清楚客观的认识上的。我在《给心理治疗师的礼物》上曾经看到这样的话“心理治疗师必须熟悉自己阴暗的一面，必须能够理解所有人类的欲望和冲动。”同时在讨论心理治疗师的风险时，作者也这样说道：“他们厌倦了公众的不合理恐惧或者贬低，也厌倦了他人的过度褒奖。”而这样的风险，在村上身上已经发生。相对于与人沟通，他似乎更乐意去观察人。因为在他用文字与思索对人施予人性关怀时，可以收到很大的成效，即很多人因为他的作品去思考人的脆弱，转而对人性充满关怀而不再那么苛责。但他在现实与人建立关系时，却似乎没有这样大的影响力，或者说，他自己都隐藏了对别人的关怀，但是这是人的一种自然的自我保护，一点都没错。

多一个村上这样的作家，是社会的一件幸事。就《挪威的森林》而言，有人说它是村上的自传文章，而村上也确实在书的开头写道：献给一些死去的朋友。有人说村上是一个为自己写作的作家，而这样的作家写出来的书是很真诚的。他在写自身的同时，背后是整个人类，所以这样的书就很有意义。村上在一开始写直子，写井，写木月。那些看似痛苦阴郁离奇的青春，实则是所有人都要经历的。有些深刻的问题，一般人只是逃避而已。或许时间会让这个问题不再纠缠，但是更多的时候，它会化成青春留在人心中的负疚，这是人活在当下最沉重的负担。为什么木月要自杀？直子的姐姐要自杀？直子要自杀？你当然可以回避这些问题，如果你没有真的经历这些事情，如果你担心这样的情绪会影响你，回避算得上是不错的选择。运气好可以一直到老也不被缠上。但村上的态度不同，他偏是要面对这些事实。面对这些事实并不意味着他一定要想清楚那些青春年少的人为什么要自杀，而是在这个过程中越来越体悟到人的脆弱，越来越认清那些恐惧、焦虑、内疚、困惑。人的正常状态，并不是所谓的阳光温暖，积极向上。而是在脆弱中寻找力量，在无聊中创生激情，不停地困惑与解脱，在孤独中渴望另一个孤独者的给予。认清了这些事实，一个人才可能不会伤害另一个人，才可能会有人性关怀。

武志红预言说接下来几十年将会是中国青少年自杀高发时段。前段时间微博上沸沸扬扬的学生烧书事件其实也已经在暗示这样的危险。中国崇尚精英教育，每个孩子小时候的理想大概都是当科学家，主席什么的，你要是想当歌星，都可能会被鄙视一下。这就会给很多，或者说绝大多数成不了精英的普通中国人一种强烈的心理落差。另一方面，中国缺乏村上那样缺乏人性关怀的作家。在追求伟大追求成功的社会氛围下，失败者要么会觉得自己是异类而异常痛苦，要么干脆和其他的一群失败者一起愤世嫉俗，但他们的骨子里，还是崇尚成功与伟大，不愿正视那个卑微渺小的自己。但似乎宣扬人性关怀不符合一个“积极向上”的社会的标准，所以我觉得武志红的预言将不可避免地实现。

其实早在我还在休学时就想把休学这一年的经历记录下来，而我也非常确认这是一件对我来说很有意义的事情。

看似是荒废的一年，就像中国经历的十年文革，以及三十年来的改革开放。这样的时间里，一些问题不再是减缓我的步伐，而是挡在我面前，不解决就寸步难行。

最初觉得问题严重是从高二下学期初开始。那个时候进了学校搞的前五十周末班，就是第一个周末，我的腿就在打篮球时骨折了。那段时间，心情是低落的，每天早上起来就唱寻寻觅觅，冷冷清清。那段时间附近，我每天早上起来晨读疯狂英语，晚上还要参加化学竞赛和数学竞赛辅导。每次上辅导课的时候我都特别困，但是，那个时候，我的一个总体思想大背景就是很想学好。因此这样的挣扎是很痛苦的，身心的。后来化学竞赛考试的时候，我的第一次小崩溃来了，几乎是什么都不会，脑子一片空白，人处于一种很难受又什么都说不清的状态。在经过十来分钟的挣扎之后，我无奈地选择放弃，交卷离场。后来数学竞赛头晕忽忽的，考完以后马上就请假了。老爸老妈带我去一个小诊所看了下，大概就是感冒，鼻炎之类的小毛病，医生说。于是我吃了点药就会学校了，期待下午学习状态就会好起来。但是接下来的状态一直差强人意。所以就开始陆续请假看病了。这个过程很长，很无奈。每次都是希望到失望。而诊断从鼻炎到颈椎病到睡眠功能异常到植物性神经功能紊乱各种各样，最后被一一排除。医生从小诊所到老中医到一二医到七枫巷到最后的北京同仁堂，大多数都擅长打马虎眼，只有北京的那位老先生坚定地跟我说，小伙子，你身体没有毛病。这家伙多少还有点医德。而这样盲目求医的过程是很长的，一直到休学结束前两个月左右。

那个时候真是相当焦虑，一方面非常想学好，一方面学习状态非常差，另一方面苦于找不到解决问题的办法。现在看来，那可以说是自己深层意愿与大脑执行想法的强烈冲突吧。

后来试过通校俩礼拜，没什么实质性作用。

国庆在西餐厅干杂活，有一整天是在碗间洗碗刷盘的。此工作不累，但是无聊。于是我自然地哼起了歌，突然之间我想起《春光乍泻》中张震边唱歌边洗碗的样子，以及后来他站在灯塔旁的礁石上，戴着黑色低沿帽，穿着皮衣，戴着围巾，手插口袋，遥望远方的一幕。

很自然地，我想起一年前一部接一部看电影的我自己。先是看皮特的电影，再是王家卫导的几乎所有电影。而这样一种奇特的生活方式，还是应该从我去十五中的那天开始说起。

那天我穿着黑色的训练服，迷彩短裤，顶着光光的头，以这样十分霸气的方式向新同学问好，不久我就获得了那个同样霸气的外号——大佬。我现在已经忘记是谁给我起的了。然后我就认识了朱汉章，也就是后来的b话王子。他居然有着和我极为类似的命运，同样是龙湾中学转来的休了一年学的。朱汉章第一天还是很够意思的，带我参观食堂，参观宿舍。后来我就开始认识了十五中。十五中果然是个神奇的地方。这里的班主任叫wjb ，这里的宿舍除了床什么都没有，这里送外卖政教处是默许的。

在十五中混了几天后就跟杨克闹上了，这位长得有点流氓像的政教处主任居然把我手机没收了，还不让我关机，我差点没和他打起来。回到教室后我就和朱汉章说我不想读了，回家自学，搞得朱汉章一愣一愣的。晚上回家我就上网写日记骂杨克。第二天神通广大的老妈告诉我杨克是表哥同学，表哥已经打电话搞定。后来手机拿回来了，可能是因为杨克跟我哥关系真的比较好，后来碰到我都还跟我打招呼，问我最近考得怎么样。我每回都是尴尬地嗯嗯。杨克后来扇了有个学生一巴掌被警察带走，还因此见报，当时是举校欢庆，我依然尴尬。顺便说下，那篇日记已经删了。

说完杨克该说十五中保安了。因为杨克和保安属于上下级关系。杨克脾气不好，保安自然也好不到哪去。我和朱汉章天天会被保安就校服的问题被批评，还有该死的通校卡，黄的换成绿的绿的换成蓝的，办了一回又一回。还有可怜的朱汉章天天迟到，闲到蛋疼的保安居然给他取了个迟到大王的绰号。