强化学习导论学习笔记——（二）

Posted on Edited on In

2. Multi-armed Bandits

k-armed Bandit Problem，K臂老虎机

问题描述：重复面临有k种选择的情况，每一次选择之后，都会收到一个reward。这个reward服从一个跟你的选择相关的分布。你的目标是，在选择t次后，找到最大的期望reward。

为什么叫K臂老虎机：有K个单臂老虎机，每个时间节点，你可以选择K个中任意一个老虎机选择按下它的臂，然后获得一个奖励。目标自然是多次选择之后的累计奖励最大。

形式化定义：假设时刻$t$的动作是$A_t$，reward是$R_t$，定义价值函数：$q_*(a) = E[R_t|A_t=a]$。

特点：每个时刻下，$q_*(a)$是固定的，stationary。

  • 如果我们知道每个动作a对应的价值q，那么这个问题对我们来说就已经解决了，即，我们选择q最大的那个a。
  • 然而，我们并不知道实际上的q是什么，只能估计$Q_t(a)\approx q_*(a)$。
  • 在每个时间节点上，如果总是选择对应的估计Q最大的a，这被称为greedy。
  • $\epsilon$-greedy：：$1-\epsilon$的概率选择Q最大的a，$\epsilon$的概率选择其他a。
  • 估计$Q_t(a) = \frac{在时刻t之前，所有采用动作a获得的奖励之和}{在时刻t之前，采用动作a的次数}= \frac{\sum^{t-1}{i=1}R_i\cdot\mathbf{1}{A_i=a}}{\sum^{t-1}{i=1}\mathbf{1}{A_i=a}}$，被称为sample-average。

10-armed Testbed

  • 设置一个10臂老虎机作模拟。
  • 真实的价值函数$q_*(a)$服从标准高斯分布（均值是0，方差是1）。
  • t时刻的奖励$R_t$服从高斯分布，均值是$q_*(A_t)$，方差是1。
  • 可以规定每次实验做1000次选择，称为一个run。
  • 一共跑了2000个独立的run。
  • 实验结果（$\epsilon$-greedy的优越性）：

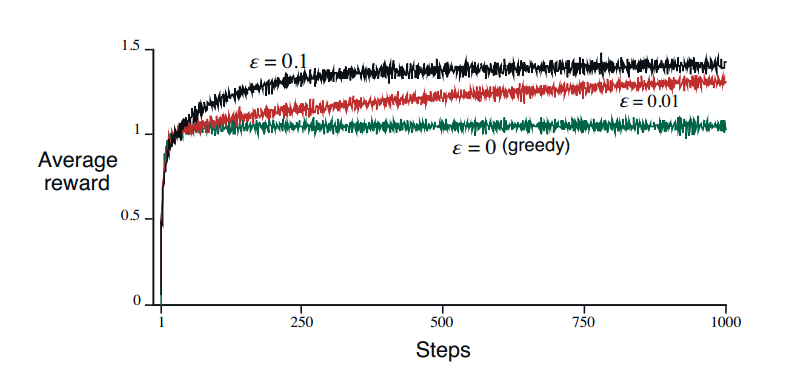
average_reward

增量式的估计

  • 上面的sample-average即：$Q_n = \frac{R_1+R_2+…+R_{n-1}}{n-1}$
  • 改写成增量式的形式：$Q_{n+1} = Q_n + \frac{1}{n}[R_n-Q_n]$
  • 即：新估计 = 老估计 + 步长 × [奖励 - 老估计]

bandit_algo

Optimistic Initial Values

  • 设置初始的$Q_1(a)$为一些较大的值。
  • 这样会鼓励explore。
  • 对于nonstationary的问题不适用。

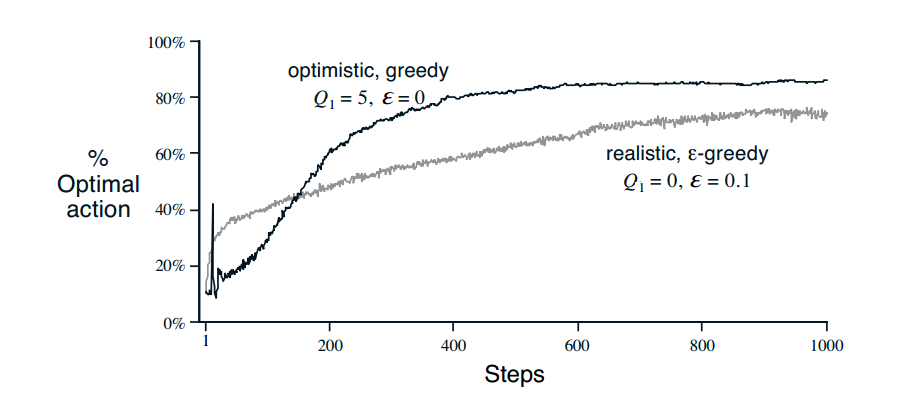
optimistic

Upper-Confidence-Bound Action Selection（UCB）

  • $A_t = \underset{a}{argmax}[Q_t(a)+c\sqrt{\frac{log;t}{N_t(a)}}]$
  • 其中，$N_t(a)$代表动作a在t之前出现的次数，根号项衡量动作a的不确定性，如果某个动作已经使用了很多次，则倾向使用使用次数少的，这样达到explore的效果。

ucb

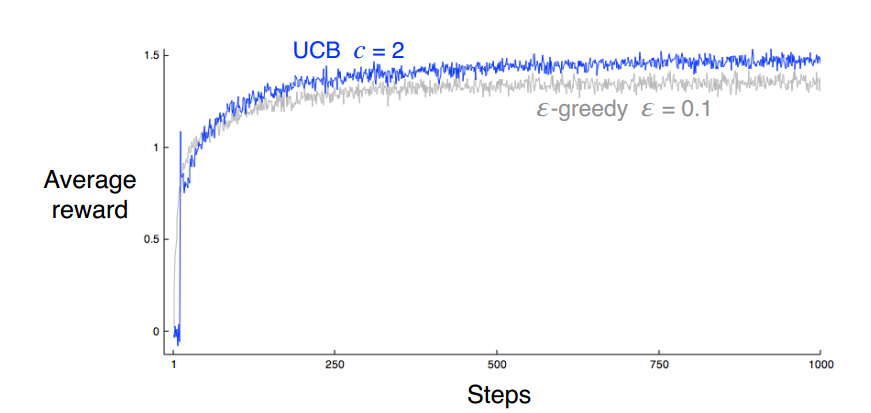
Gradient Bandit Algorithms

  • 使用一个数值表示对某个动作的偏好：$H_t(a)$
  • $Pr{A_t=a}=\frac{e^{H_t(a)}}{\sum_{b=1}^k{e^{H_t(b)}}}=\pi_t(a)$
  • 更新规则：
    • $H_{t+1}(A_t) = H_t(A_t) + \alpha(R_t-\overline R_t)(1-\pi _t(A_t))$

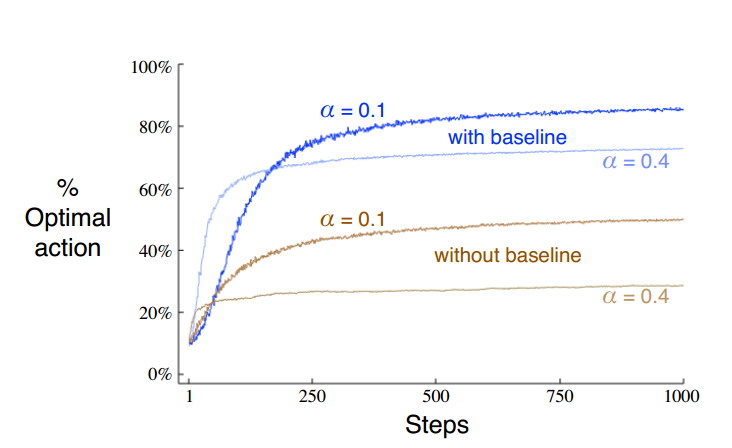
gradient_bandit

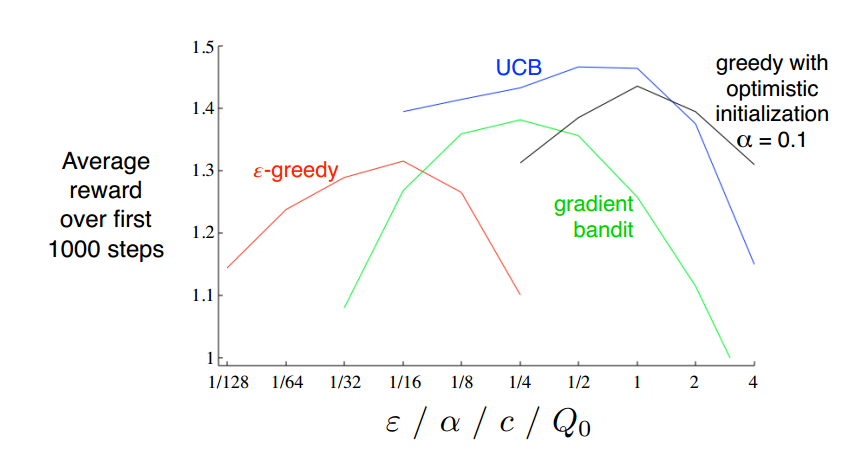
各种方法对比

bandit_methods

代码分析

完整源码

核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# get an action for this bandit
def act(self):
    if np.random.rand() < self.epsilon:
        return np.random.choice(self.indices)

    if self.UCB_param is not None:
        UCB_estimation = self.q_estimation + \
                    self.UCB_param * np.sqrt(np.log(self.time + 1) / (self.action_count + 1e-5))
        q_best = np.max(UCB_estimation)
        return np.random.choice([action for action, q in enumerate(UCB_estimation) if q == q_best])

    if self.gradient:
        exp_est = np.exp(self.q_estimation)
        self.action_prob = exp_est / np.sum(exp_est)
        return np.random.choice(self.indices, p=self.action_prob)

    q_best = np.max(self.q_estimation)
    return np.random.choice([action for action, q in enumerate(self.q_estimation) if q == q_best])

# take an action, update estimation for this action
def step(self, action):
    # generate the reward under N(real reward, 1)
    reward = np.random.randn() + self.q_true[action]
    self.time += 1
    self.average_reward = (self.time - 1.0) / self.time * self.average_reward + reward / self.time
    self.action_count[action] += 1

    if self.sample_averages:
        # update estimation using sample averages
        self.q_estimation[action] += 1.0 / self.action_count[action] * (reward - self.q_estimation[action])
    elif self.gradient:
        one_hot = np.zeros(self.k)
        one_hot[action] = 1
        if self.gradient_baseline:
            baseline = self.average_reward
        else:
            baseline = 0
        self.q_estimation = self.q_estimation + self.step_size * (reward - baseline) * (one_hot - self.action_prob)
    else:
        # update estimation with constant step size
        self.q_estimation[action] += self.step_size * (reward - self.q_estimation[action])
    return reward