强化学习导论学习笔记——（五）

Posted on Edited on In

5. Monte Carlo Methods

蒙特卡洛方法简介

使用蒙特卡洛方法不需要像DP一样，对环境要有完整的知识，而是通过经验去学习。所谓经验就是对状态、动作、奖励的采样（sample sequence）。

用sample的均值去近似期望。

使用蒙特卡洛通常需要完整的episode，因此蒙特卡洛的更新方式更像是episode-by-episode，而不是像DP的step-by-step。

优点：

  • 1.可以从实际经验中学习；
  • 2.可以从模拟的经验中学习；
  • 3.可以直接从感兴趣的state开始采样episode。

蒙特卡洛预测（评估）

  • 在一个episode中状态s可能出现多次，每一次出现称为一次对状态s的访问（visit）。
  • first-visit MC method:只是用每个episode中第一次对状态s的访问评估状态s的价值函数。
  • every-visit MC method:用每个episode中每次对状态s的访问评估状态s的价值函数。

fv_mc_est

$V(s)\leftarrow average(Return(s))$

核心代码：

1
2
3
4
5
6
7
8
9
# Monte Carlo Sample with On-Policy
def monte_carlo_on_policy(episodes):
    ...
    for i in range(0, episodes):
        # play接受一个策略，然后模拟生成一个完整的轨迹和奖励
        _, reward, player_trajectory = play(target_policy_player)
        ...
    # 返回价值函数的平均值
    return states_usable_ace / states_usable_ace_count, states_no_usable_ace / states_no_usable_ace_count

蒙特卡洛评估动作价值函数（Action Values）

  • 注意：如果我们的问题中，没有对环境建模，那么单纯评估状态价值函数是不够的。我们必须要评估动作价值函数。
  • 主体思想：从评估state到评估state-action对。
  • 可能存在的问题：某些state-action对可能不会被访问（稀疏性问题）。

蒙特卡洛控制

  • 控制（control）的目的是找到最优策略。
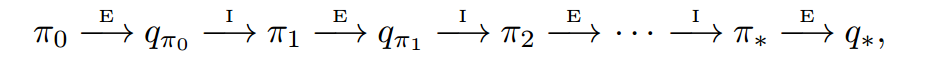
  • mc_policy_iter
  • 其中，$E$代表策略的evaluation，$I$代表策略的improvement。

Monte Carlo Exploring Starts

  • Exploring Starts：所有的state-action对都有可能被选为episode的开始（start）。

mces

核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Monte Carlo with Exploring Starts
def monte_carlo_es(episodes):
    ...
    # behavior policy is greedy
    def behavior_policy(usable_ace, player_sum, dealer_card):
        ...
        # get argmax of the average returns(s, a)
        values_ = state_action_values[player_sum, dealer_card, usable_ace, :] / \
                  state_action_pair_count[player_sum, dealer_card, usable_ace, :]
        return np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])

    # play for several episodes
    for episode in range(episodes):
        # for each episode, use a randomly initialized state and action
        initial_state = [bool(np.random.choice([0, 1])),
                       np.random.choice(range(12, 22)),
                       np.random.choice(range(1, 11))]
        initial_action = np.random.choice(ACTIONS)
        current_policy = behavior_policy if episode else target_policy_player
        _, reward, trajectory = play(current_policy, initial_state, initial_action)
        ...

    return state_action_values / state_action_pair_count

不使用Exploring Starts

  • 如何才能不使用Exploring Starts？保证所有被选择的动作被持续地选择。
  • 使用on-policy和off-policy。

on-policy vs off-policy

  • on-policy只有一套policy，更简单，是首选。
  • off-policy使用两套policy，更复杂、更难收敛；但也更通用、更强大。
  • on-policy和off-policy本质依然是Exploit vs Explore的权衡。

on-policy

  • 去评估和提高生成episode时采用的policy。全过程只有一种策略，MC ES属于on-policy。

off-policy

  • 所有的MC控制方法都面临一个困境：它们都想找到一个最优的策略，但却必须采用非最优的策略去尽可能多地探索（explore）数据。
  • 直接使用两套策略：采样用的policy称为behavior policy，即行为策略；最终的目标policy：target policy，即目标策略。这就是off-policy。
  • 假设目标策略是$\pi$，行为策略是$b$，那么对于所有的$\pi(a|s)>0$必然有$b(a|s)>0$，这称为“覆盖”（coverage）。一个常见的例子是：行为策略使用价值函数的greedy policy，而目标策略使用ε-greedy policy。

重要性采样（importance sampling）

几乎所有的off-policy都使用重要性采样（importance sampling）。

为什么要使用重要性采样？我们希望在使用目标策略$\pi$的情况下用均值估计价值的期望，但我们获得的是在使用行为策略$b$的情况下的均值，也就是：$\mathbb{E}[G_t \mid S_t =s] = v_b(s)$。这二者是有差距的。因此我们希望使用重要性采样去纠正。

给定初始状态$S_t$，后续的状态-动作轨迹在使用目标策略$\pi$的情况下的概率为：
$Pr{At,S_{t+1}, A_{t+1}, … S_T \mid S_t, A_{t:T −1} \sim \pi}$ $=\prod_{k=t}^{T-1}\pi(A_k\mid S_k)p(S_{k+1}\mid S_k, A_k)$

引入重要性采样比例（the importance sampling ratio）：
$\rho_{t:T −1}=\frac{\prod_{k=t}^{T-1}\pi(A_k\mid S_k)p(S_{k+1}\mid S_k, A_k)}{\prod_{k=t}^{T-1}b(A_k\mid S_k)p(S_{k+1}\mid S_k, A_k)}$ $=\prod_{k=t}^{T-1}\frac{\pi(A_k\mid S_k)}{b(A_k\mid S_k)}$
上面这个式子正好巧妙地把MDP中未知的状态转移概率约掉。

于是return的期望又可以得到校正：$\mathbb{E}[\rho_{t:T−1}G_t \mid S_t =s] = v_{\pi}(s)$

odinary importance sampling：

$$V(s) = \frac{\sum_{t\in J(s)} \rho_{t:T (t)-1}Gt}{\mid J(s)\mid} $$

weighted importance sampling：

$$V(s) = \frac{\sum_{t\in J(s)} \rho_{t:T (t)-1}Gt}{\sum_{t\in J(s)} \rho_{t:T (t)-1}} $$

odinary importance sampling vs. weighted importance sampling:

  • odinary importance sampling：无偏差，但方差没有保证。
  • weighted importance sampling：有偏差，方差有上限。

评估：

off_policy_mc_prediction

上面的评估使用了采样权重增量式的方法。

控制：

off_policy_mc_control

核心代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# Monte Carlo Sample with Off-Policy
def monte_carlo_off_policy(episodes):
    initial_state = [True, 13, 2]

    rhos = []
    returns = []

    for i in range(0, episodes):
        _, reward, player_trajectory = play(behavior_policy_player, initial_state=initial_state)

        # get the importance ratio
        numerator = 1.0
        denominator = 1.0
        for (usable_ace, player_sum, dealer_card), action in player_trajectory:
            if action == target_policy_player(usable_ace, player_sum, dealer_card):
                denominator *= 0.5
            else:
                numerator = 0.0
                break
        rho = numerator / denominator
        rhos.append(rho)
        returns.append(reward)

    rhos = np.asarray(rhos)
    returns = np.asarray(returns)
    weighted_returns = rhos * returns

    weighted_returns = np.add.accumulate(weighted_returns)
    rhos = np.add.accumulate(rhos)

    ordinary_sampling = weighted_returns / np.arange(1, episodes + 1)

    with np.errstate(divide='ignore',invalid='ignore'):
        weighted_sampling = np.where(rhos != 0, weighted_returns / rhos, 0)

    return ordinary_sampling, weighted_sampling