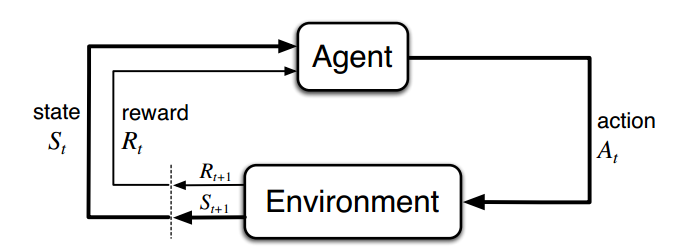
强化学习导论学习笔记——(二)
Python正则表达式梳理
最近在一个项目中大量使用正则表达式,对各种用法做个梳理。
简介
正则表达式的作用是检查一个字符串是否与某种模式匹配。Python中的re模块提供正则匹配相关的方法。
语法
Python正则表达式测试网站:https://pythex.org/
Tensorflow动态seq2seq使用总结(r1.3)
动机
其实差不多半年之前就想吐槽Tensorflow的seq2seq了(后面博主去干了些别的事情),官方的代码已经抛弃原来用静态rnn实现的版本了,而官网的tutorial现在还是介绍基于静态的rnn的模型,加bucket那套,看这里。

看到了吗?是legacy_seq2seq的。本来Tensorflow的seq2seq的实现相比于pytorch已经很复杂了,还没有个正经的tutorial,哎。
好的,回到正题,遇到问题解决问题,想办法找一个最佳的Tensorflow的seq2seq解决方案!
学习的资料
- 知名博主WildML给google写了个通用的seq2seq,文档地址,Github地址。这个框架已经被Tensorflow采用,后面我们的代码也会基于这里的实现。但本身这个框架是为了让用户直接写参数就能简单地构建网络,因此文档没有太多参考价值,我们直接借用其中的代码构建自己的网络。
- 俄罗斯小伙ematvey写的:tensorflow-seq2seq-tutorials,Github地址。介绍使用动态rnn构建seq2seq,decoder使用
raw_rnn,原理和WildML的方案差不多。多说一句,这哥们当时也是吐槽Tensorflow的文档,写了那么个仓库当第三方的文档使,现在都400+个star了。真是有漏洞就有机遇啊,哈哈。
条件随机场 CRF总结和实现
概率无向图模型
回顾一下之前讲解的概率无向图模型:https://applenob.github.io/machine_learning/graph.html
总结一下:
- 最大团:无向图$G$中任何两个结点都有边连接的结点子集称为团(clique)。若团$C$不能在加入任何一个结点使其称为一个更大的团,则称$C$为图$G$的一个最大团。
- 概率无向图模型的联合概率分布可以表示成其最大团上的随机变量的函数的乘积形式。这也被称为概率无向图模型的因子分解。
- $P(Y) = \frac{1}{Z}\prod_C\psi_C(Y_C)$,其中,$Z$是规范化因子,$Z = \sum_Y\prod_C\psi_C(Y_C)$,$\psi_C(Y_C)$称为势函数,要求势函数是严格正的(因为涉及到累乘)。
条件随机场
Max Entropy学习总结
模型推导
最大熵是选择最优模型的一个准则,即,首先要满足已有的事实(约束条件),然后在没有更多信息的情况下,那些不确定的部分都是“等可能的”。“等可能”本身不容易操作,熵是一个可以优化的数值目标。
这里最大熵最大化的,是条件熵$H(Y|X)$。
$$H(Y|X)=-\sum_{x,y}\hat{P}(x)P(y|x)logP(y|x)$$
具体的关于信息熵的文章,可以看colah的这篇博客,里面对信息熵/互信息/条件熵的物理意义做很好的解释。
一个简单的生成式依存句法解析器
这篇博客中,我通过学习hankcs的Java版本,自己试着做一个简单的Python版本,用于学习和理清思路。
思路
所谓生成式句法解析是指生成一些列依存句法树,挑出概率最大的一棵。
这里的实现考虑了词性信息+词汇信息,使用最大生成树Prim算法搜索最终结果,实现一个简单的汉语依存句法分析器。
具体:
N-最短路径方法的分词实现
这篇文章是我照着《基于N最短路径方法的中文词语粗分模型》这篇论文,自己用Python实现了下文中的算法,用于理解原理。
大致思想
考虑到汉语自动分词中存在切分歧义消除和未登录词识别两个主要问题,因此,有专家将分词过程分成两个阶段:首先采用切分算法对句子词语进行初步切分,得到一个相对最好的粗分结果,然后,再进行歧义排除和未登录词识别。
N-最短路径方法就是一种词语粗分模型,大致步骤:
- 1.根据词典,找出字串中所有可能的词,构造词语切分有向无环图。
- 2.每个词对应图中的一条有向边,并赋给相应的边长(权值) 。
- 3.然后针对该切分图,在起点到终点的所有路径中,求出长度值按严格升序排列(任何两个不同位置上的值一定不等)依次为第1、第2、…、第i、…、第N(N≥1)的路径集合作为相应的粗分结果集。
- 4.如果两条或两条以上路径长度相等,那么它们的长度并列第i,都要列入粗分结果集,而且不影响其他路径的排列序号,最后的粗分结果集合大小大于或等于N。
具体介绍
基于统计学的的分词
最大匹配分词方法只考虑词有没有在字典中出现,没有考虑词在词典中的频率。
基于统计学的分词即考虑词在词典中的频率的一种简单的分词方法。
注:下面的代码参考snownlp作者的博客:http://www.isnowfy.com/python-chinese-segmentation/
1 | import math |
小插曲: